高二数学同步测试—平面和平面的位置关系（3）
一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知直线l⊥平面
，直线m
平面
，则下列命题中正确的是 （ ）
A．
B．
C．
D．
2．在下列条件中，可判断平面α与β平行的是 （ ）
A．α、β都垂直于平面r.
B．α内存在不共线的三点到β的距离相等.
C．l，m是α内两条直线，且l∥β，m∥β.
D．l，m是两条异面直线，且l∥α，m∥α, l∥β，m∥β.
3．下列命题正确的是 （ ）
A. 过平面外的一条直线只能作一平面与此平面垂直
B. 平面
⊥平面
于
，
，
，则
C. 一直线与平面的一条斜线垂直，则必与斜线的射影垂直
D. 
、
、
是两两互相垂直的异面直线，
为、的公垂线，则∥
4．将边长为的正方形
沿对角线
折起，使得
，则三棱锥
—
的体积为 （ ）
A.
B.
C.
D.
5．在空间四边形ABCD中，AB=BC=CD=DA， E∈AB,F∈CD 且AE：EB=CF：FD= λ
（0＜ λ ＜1 ＝ 设EF与AC、BD所成的角分别是 α 、 β ，则 α+β= （ ）
A.大于90° B.小于90° C.等于90° D.与 λ 的值有关
6．把正方体各个面伸展成平面，则把空间分为的部分数值为 ( )
A．13 B．19 C．21 D．27
7．已知α，β是平面，m，n是直线.下列命题中不正确的是 （ ）
A．若m∥n，m⊥α，则n⊥α B．若m∥α，α∩β=n，则m∥n
C．若m⊥α，m⊥β，则α∥β D．若m⊥α，
，则α⊥β
8．已知平面
平面
,直线
且
则 （ ）
A．内必存在直线与
平行，且存在直线与垂直
B．内不一定存在直线与平行，但必存在直线与垂直
C．内不一定存在直线与平行，且不存在直线与垂直
D．内必存在直线与平行，但不存在直线与垂直
9．两个完全相同的长方体的长、宽、高分别为5cm，4cm，3cm，把它们重叠在一起组成一个新长方体，在这些新长方体中，最长的对角线的长度是（ ）
A. 
B.
C.
D.
10．已知AB是异面直线a、b的公垂线段，AB=2，且a与b成30°角，在直线a上取AP=4，则点P到直线b的距离为 （ ）
A．
B．4 C．2
D．或2
11．二面角α—l—β的棱l上有一点P，射线PA在α内，且与棱l成45°角，与面β成
|
A．30°或150° B．45°或135° C．60°或120° D．90°
12．在矩形ABCD中，AB=a，AD=2b，a<b，E、F分别是
AD、BC的中点，以EF为折痕把四边形EFCD折起，
当
时，二面角C—EF—B的平面角的余
弦值等于 （ ）
A．0 B．
C．
D．
二、填空题：本大题满分16分，每小题4分，各题只要求直接写出结果.
13．设
是直二面角，
∠BAN=∠CAN=45°，则∠BAC=_____________．
14．在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB2+AC2=BC2.”拓展到空间，类比平面几何的勾股定理，研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是：“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直，则 ”．
15．与正方形各面成相等的角且过正方体三个顶点的截面的个数是________．
16．
、是两个不同的平面，、
是平面及之外的两条不同直线，给出四个论断：
①⊥ ②⊥ ③⊥ ④⊥
以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题： _________________________.
三、解答题：本大题满分74分.
17．（本小题满分10分）已知矩形ABCD的边AB=1，BC=a，PA⊥平面ABCD，PA=1，问
|
|
D是CB延长线上一点，且BD=BC.
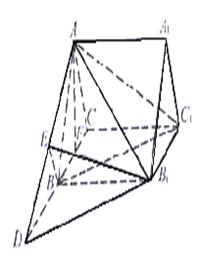
（Ⅰ）求证：直线BC1//平面AB1D；
（Ⅱ）求二面角B1—AD—B的大小；
（Ⅲ）求三棱锥C1—ABB1的体积.
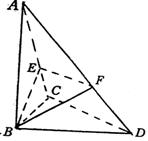
19．（本小题满分12分）已知空间四边形ABCD的边长都是1，又BD=
，当三棱锥A—BCD的体积最大时，求二面角B—AC—D的余弦值．
20．（本小题满分12分）
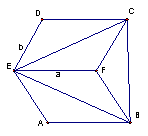
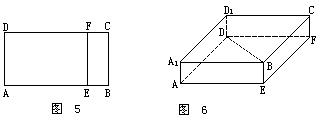
有一矩形纸片ABCD，AB=5，BC=2，E，F分别是AB，CD上的点，且BE=CF=1，把纸片沿EF折成直二面角．
（1）求BD的距离；
（2）求证AC，BD交于一点且被这点平分．
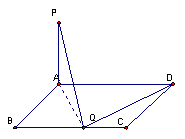
21．（本小题满分12分）已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，
∠ADB=60°，E、F分别是AC、AD上的动点，且
|
（Ⅱ）当λ为何值时，平面BEF⊥平面ACD？
|
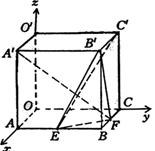
（Ⅰ）求证：A′F⊥C′E；
（Ⅱ）求二面角B′—EF—B的大小.
参考答案
一． 选择题
1．A 2．D 3．D 4．D 5．C 6．D 7．D 8．B 9．C 10．A 11．B 12．C
4．解：取BD的中点为O，BD⊥平面OAC，
，则
=
。选D
12．解 由图可知 CE=BE=
当时，CB=
。 
为所求平面角，由余弦定理得cos
。 选（C）。
二、填空题
13．60°； 14. 
；
15．解：如图中，截面ACD1和截面ACB1均符合题意要求，这样的截面共有8个；
16．
或
.
三、解答题
17．解：连接AQ，因PA⊥平面ABCD，所以PQ⊥QD
AQ⊥QD，即以AD为直经的圆与BC有交点．
当AD=BC=a
AB=1,即a1时，在BC边上存在点Q，使得PQ⊥QD；．．．．．．．．．5分
当0<a<1时，在BC边上不存在点Q，使得PQ⊥QD．．．．．．．．．．．．．．．．．．．．．．10分
18．（Ⅰ）证明：CD//C1B1，又BD=BC=B1C1， ∴ 四边形BDB1C1是平行四边形， ∴BC1//DB1.
又DB1平面AB1D，BC1
平面AB1D，∴直线BC1//平面AB1D.．．．．．．．．．．．．．．．．．．．5分
（Ⅱ）解：过B作BE⊥AD于E，连结EB1， ∵B1B⊥平面ABD，∴B1E⊥AD ，
|
∴∠B1EB是二面角B1—AD—B的平面角， ∵BD=BC=AB， ∴E是AD的中点， 
在Rt△B1BE中，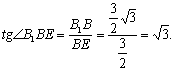
∴∠B1EB=60°。即二面角B1—AD—B的大小为60°…………10分
（Ⅲ）解法一：过A作AF⊥BC于F，∵B1B⊥平面ABC，∴平面ABC⊥平面BB1C1C，
∴AF⊥平面BB1C1C，且AF=
即三棱锥C1—ABB1的体积为
…………15分
解法二：在三棱柱ABC—A1B1C1中，
即为三棱锥C1—ABB1的体积．
19．解 如图，取AC中点E，BD中点F，由题设条件知道
（1）
BED即二面角B—AC—D的平面角．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分
（2）当AF
面BCD时，VA—BCD达到最大．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分
这时ED2=AD2-AE2=1-AE2=1-
=1-
=1-
，
又 BE2=ED2，
∴ cos
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分
A
E
B F D
C
20．分析：将平面BF折起后所补形成长方体AEFD-A1BCD1，则BD恰好是长方体的一条对角线．
（1）解：因为AE，EF，EB两两垂直，
所以BD恰好是以AE，EF，EB为长、宽、高的长方体的对角线，
．．．．．．．．．．．．．．．．6分
（2）证明：因为AD 
EF，EF BC，所以AD BC．
所以ACBD在同一平面内，
且四边形ABCD为平行四边形．
所以AC、BD交于一点且被这点平分．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分
21．证明：（Ⅰ）∵AB⊥平面BCD， ∴AB⊥CD，
∵CD⊥BC且AB∩BC=B， ∴CD⊥平面ABC.………………………………3分
又
∴不论λ为何值，恒有EF∥CD，∴EF⊥平面ABC，EF平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC…………．．．．．．．．．．．．．．．．．．．．6分
（Ⅱ）由（Ⅰ）知，BE⊥EF，又平面BEF⊥平面ACD，
∴BE⊥平面ACD，∴BE⊥AC.………………8分
∵BC=CD=1，∠BCD=90°，∠ADB=60°，
∴
由AB2=AE·AC 得
故当
时，平面BEF⊥平面ACD.………………………………………………12分
22．证明：（Ⅰ）
、
、
，
……4分
.……………………………6分
（Ⅱ）取EF的中点M，连BM⊥EF，根据三垂线定理知EF⊥B′M，
即为二面角B′—EF—B的平面角．．．．．．．．．．．．．．．．．．．．．．．．．10分
在Rt△BMF中，
在Rt△B′BM中，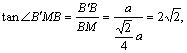
∴二面角B′—EF—B的大小是
.……………………………………13分
审定意见：试题整体质量较高，新换了一道考能力的活题，对试题中的个别文字、标点符号进行了修改。
审稿人：安振平