高二数学同步测试—球(5)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题①多面体的面数最少为4;②正多面体只有5种;③凸多面体是简单多面体;④一个几何体的表面,经过连续变形为球面的多面体就叫简单多面体。其中正确的个数为( )
A.1 B.2 C.3 D.4
2.球的体积是![]() π,则此球的表面积是 ( )
π,则此球的表面积是 ( )
A. 12π B. 16π
C. ![]() π D.
π D. ![]() π
π
3.下列四个命题中,其中错误的个数是 ( )
①经过球面上任意两点,可以作且只可以作一个大圆;
②经过球直径的三等分点,作垂直于该直径的两个平面,则这两个平面把球面分成三部分的面积相等;
③球的面积是它大圆面积的四倍;
④球面上两点的球面距离,是这两点所在截面圆上,以这两点为端点的劣弧的长.
A. 0 B. 1 C. 2 D. 3
4.球面上有3点,其中任意两点的球面距离都等于大圆周长的![]() ,经过这3点的小圆的周长为
,经过这3点的小圆的周长为![]() ,那么这个球的半径为 ( )
,那么这个球的半径为 ( )
A.![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
5.球的体积是![]() π,则此球的表面积是 ( )
π,则此球的表面积是 ( )
A. 12π B. 16π C. ![]() π D.
π D. ![]() π
π
6.一个四面体的所有棱长都为![]() ,四个顶点在同一球面上,则此球的表面积为 ( )
,四个顶点在同一球面上,则此球的表面积为 ( )
A.3π B.4π C.![]() D.6π
D.6π
7.64个直径都为![]() 的球,记它们的体积之和为
的球,记它们的体积之和为![]() ,表面积之和为
,表面积之和为![]() ;一个直径为a的球,记其体积为
;一个直径为a的球,记其体积为![]() ,表面积为
,表面积为![]() ,则 ( )
,则 ( )
A. ![]() >
>![]() 且
且![]() >
>![]() B.
B. ![]() <
<![]() 且
且![]() <
<![]()
C. ![]() =
=![]() 且
且![]() >
>![]() D.
D. ![]() =
=![]() 且
且![]() =
=![]()
8.设地球的半径为R,在纬度为![]() 的纬线圈上有A,B两地,若这两地的纬线圈上的弧长为
的纬线圈上有A,B两地,若这两地的纬线圈上的弧长为 ![]() ,则A,B两地之间的球面距离为 ( )
,则A,B两地之间的球面距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.一根细金属丝下端挂着一个半径为1cm的金属球,将它浸没底面半径为2cm的圆柱形容器内的水中,现将金属丝向上提升,当金属球被拉出水面时,容器内的水面下降了( )
A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D.
cm D. ![]() cm
cm
10.地球半径为R, 北纬45°圈上A,B两点分别在东径130°和西径140°, 并且北纬45°圈小圆的圆心为O´, 则在四面体O-ABO´中,直角三角形有 ( )
A.0个 B.2个 C. 3个 D.4个
11.定义1分的地球球心角所对的地球大圆弧长为1海里.在北纬45°圈上有甲、乙两地,甲地位于东经120°,乙位于西经150°,则甲乙两地在球面上的最短距离为 ( )
A.5400海里 B.2700海里 C.4800海里 D.3600海里
12.甲球与某立方体的各个面都相切,乙球与这个立方体的各条棱都相切,丙球过这个立方体的所有顶点,则甲、乙、丙三球的半径的平方之比为 ( )
A.1∶2∶3 B.1∶![]() ∶
∶![]()
C.1∶![]() ∶
∶![]() D.1∶2
D.1∶2![]() ∶3
∶3![]()
二、填空题:本大题满分16分,每小题4分,各题只要求直接写出结果.
13.两个半径为1的铁球,熔化成一个球,这个球的半径是 .
14.球的半径为8,经过球面上一点作一个平面,使它与经过这点的半径成45°角,则这个平面截球的截面面积为 .
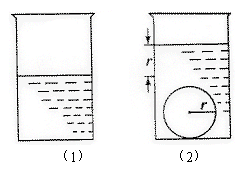 15.如图,一个底面半径为R的圆柱形量杯中装有
15.如图,一个底面半径为R的圆柱形量杯中装有
适量的水.若放入一个半径为r的实心铁球,水
面高度恰好升高r,则![]() .
.
16.湖结冰时,一个球漂在其上,取出后(未弄破冰),
冰面上留下了一个直径为24cm,深为8cm的空穴,
则该球的半径为 .
三、解答题:本大题满分74分.
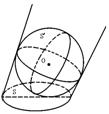 17.(12分)在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为
17.(12分)在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为![]() 米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
18.(12分) 把四个半径为R的小球放在桌面上,使下层三个,上层一个,两两相切,求上层小球最高处离桌面的距离.
19.(12分)A、B、C是球O表面上三点,AB=6㎝,∠ACB= 30°,点O到△ABC所在截面的距离为5㎝,求球O的表面积.
20.(12分)如果球、正方体与等边圆柱(底面直径与母线相等)的体积相等,求它们的表面积![]() 的大小关系.
的大小关系.
21.(12分)球O的半径为R,A﹑B﹑C在球面上,A与B,A与C的球面距离都为![]() ,B与C的球面距离为
,B与C的球面距离为![]() ,求球O在二面角B-OA-C内的部分的体积.
,求球O在二面角B-OA-C内的部分的体积.
22.(14分)同底的两个正三棱锥内接于半径为R的球,它们的侧面与底面所成的角分别为![]() 求:
求:
(1) 侧面积的比;
(2) 体积的比;
(3)
角![]() 的最大值.
的最大值.
参考答案
一、选择题:
1.D 2.B 3.C 4.B 5.B 6.A 7.C 8.D 9.D 10.C 11.D 12. B
1解:据多面体的概念选D.
6解:已该正四面体的六条棱为面对角线的正方体的棱长为1,这里的正四面体与正方体的外接球相同,故其外接球的直径为![]() ,其表面积为
,其表面积为![]() .选A.
.选A.
7解: ![]() =
=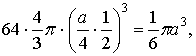
![]() =
=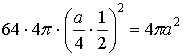 .
.
![]() =
= 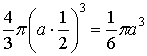 ,
, ![]() =
=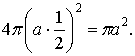
∴![]() =
=![]() ,
, ![]() >
>![]() .选C.
.选C.
8.解:设球心为O,纬度为![]() 的纬线圈的圆心为O´,则∠O´AO=
的纬线圈的圆心为O´,则∠O´AO=![]() ,∴O´A=OAcos∠O´AO=Rcos
,∴O´A=OAcos∠O´AO=Rcos![]() ,设A,B两地间的径度差的弧度数为
,设A,B两地间的径度差的弧度数为![]() ,则
,则
![]() Rcos
Rcos![]() =
=![]() , ∴
, ∴![]() =
=![]() , 即A,B两地是⊙O´的一条直径的两端点,∴∠AOB=
, 即A,B两地是⊙O´的一条直径的两端点,∴∠AOB=![]() ,
,
∴A,B两地之间的球面距离为![]() . 答案:D.
. 答案:D.
9.解:球的体积等于水下降的体积即![]()
![]() ,
,![]() .答案:D.
.答案:D.
二、填空题
13.![]() 14.
14.![]() 15.
15. ![]() 16.13cm.
16.13cm.
16.解: 设球的半径为R,依题意知截面圆的半径r=12,球心与截面的距离为d=R-8,由截面性质得:r2+d2=R2,即122+(R-8)2=R2. 得R=13 ∴该球半径为13cm.
三、解答题
17. 解:由题意知,光线与地面成60°角(2 分),设球的阴影部分面积为S,垂直于光线的大圆面积为
S′(6分),则Scos30°=S′(9分),并且S′=9π,所以S=6![]() π(米2)……
12分
π(米2)……
12分
18 . (2+![]() )R
)R
解: 将四个球心两两连结(2分),构成一个棱长为2R的正四面体![]() (4分)
(4分)
设底面正三角形![]() 的中心为H, 则
的中心为H, 则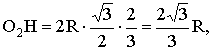 (8分)
(8分)
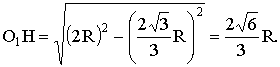 (10分)
(10分)
故上层小球最高处离桌面的距离为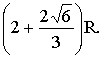 (12分)
(12分)
19.解:![]()
20. 解:设球的半径为R、正方体的棱长为a , 等边圆柱的底面半径为r, 且它们的体积都为V, (2分)则: V=![]() , (5分)
, (5分) 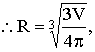
![]()
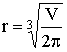 .(8分)
.(8分)
![]()
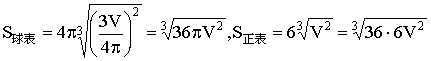
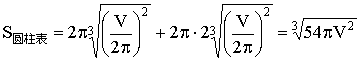 ,(10分)
,(10分)
![]() .(12分)
.(12分)
21.解:A与B,A与C的球面距离都为![]() ,(2分)
,(2分)![]() ,(6分)
,(6分)![]() BOC为二面角B-AO-C的平面角,(8分)
BOC为二面角B-AO-C的平面角,(8分)
又B与C的球面距离为![]() ,
,![]() BOC=
BOC=![]() ,(10分)
,(10分)![]() 球O夹在二面角B-AO-C的体积是球的六分之一即为
球O夹在二面角B-AO-C的体积是球的六分之一即为![]() (12分)
(12分)
22.解:(1)设O为球心,![]() 为正三棱锥底面ABC所在圆的圆心,两个三棱锥的顶点分别为P,Q, 取BC的中点D,则
为正三棱锥底面ABC所在圆的圆心,两个三棱锥的顶点分别为P,Q, 取BC的中点D,则![]()
![]()
![]() 是侧面与底面所成二面角的平面角,(1分)
是侧面与底面所成二面角的平面角,(1分)
![]()
![]()
![]() ,同理
,同理![]() =
=![]() .(2分)
.(2分)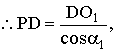
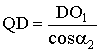 ,
,
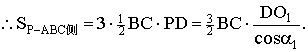
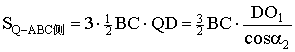 .(4分)
.(4分)
![]() :
:![]()
![]() =
=![]() .(5分)
.(5分)
(2)![]() ,(7分)
,(7分)
这两个三棱锥的底都是三角形![]() ,
,
![]() (9分)
(9分)
(3)设![]() 边长为a,
边长为a,![]() ,则
,则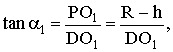
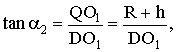 (11分)而
(11分)而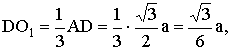
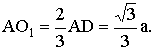
![]() (12分)
(12分)
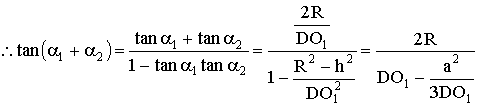
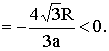 (13分)
(13分)
![]() 当平面ABC通过球心O时,a最大为
当平面ABC通过球心O时,a最大为![]()
![]() 时,
时,
![]() 取最大值
取最大值![]() ,这时
,这时![]() 也最大,最大值为
也最大,最大值为![]() .(14分)
.(14分)
审定意见:本套试题整体质量比较高,尽对试题中的个别文字、标点符号进行了修改。
审稿人:安振平