高中学生学科素质训练
高二数学同步测试—直线和平面的位置关系（2）
一、选择题（本题每小题5分，共60分）
1．当太阳光线与水平面的倾斜角为60°时，要使一根长为
与水平地面所成的角为 （ ）
A．15° B．30° C．45° D．60°
2．正方体ABCD-A1B
； C．
； D．
．
3．长方体ABCD-A1B
为α、β，面对角线BC1与面ABCD所成的角为γ，则有 ( )
A．sinα=sinβsinγ B．cosα=sinβcosγ
C．cosα=cosβcosγ D．sinα=cosβsinγ
4．空间四边形的与各顶点等距离的截面共有 ( )
A．7个 B．4个 C．3个 D．1个
|
|
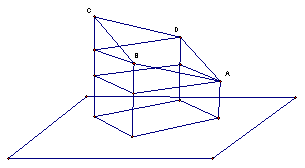
5．图中给出的是长方体形木料想象沿图中平面所示位置截长方体，若那么截面图形是下面四个图形中的
A B C D
6．RtΔABC的斜边BC在平面α内，AÏα，设A在α上的射影为A’，则由A'B,A'C,BC组成的图形是 （ ）
A．直角三角形 B．锐角三角形
C．线段或锐角三角形 D．线段或钝角三角形
7．正方体最长的对角线所在的直线与正方体各条棱所成的角的弧度值的种数是 （ ）
A．1 B．
8．空间五个点，其中任意两点的连线都与其他三个点确定的平面垂直，则这五个点（ ）
A．存在，且其中任意四个点不共面. B．存在，其中可能有四个点共面.
C．不存在，但在任意两个点确定的10条直线中可以有8条分别与另外三个点确定的平面垂直.
D．不存在，且在任意两个点确定的10条直线中至少有7条分别与另外三个点确定的平面垂直.
9．设P是平面α外一点，且P到平面α内的四边形的四条边的距离都相等，则四边形是 。
A．梯形 B．圆外切四边形 C．圆内接四边形 D．任意四边形
10．若a，b是异面直线，P是a，b外的一点，有以下四个命题：
①过P点可作直线k与a，b都相交。
②过P点可作平面与a，b都平行。
③过P点可作直线与a，b都垂直。
④过P点可作直线k与a，b所成角都等于50
。这四个命题中正确命题的序号是（ ）
A．①、②、③。 B．②、③、④。 C．②。 D．③、④。
11．若一个长方体共点的三个表面的对角线长分别为a、b、c ，则长方体的对角线长是（ ）
A．
B．
C．
D．
12．已知四棱锥底面四边形中顺次三个内角的大小之比为2：3：4，此棱锥的侧棱与底面所成的角相等，则底面四边形的最小角是 （ ）
A．
B． C．
D．无法确定的。
二、填空（本题每小题4分，共16分）：
13．若两直线a,b在平面α上的射影a',b'是平行的直线，则a,b的位置关系是 ．
14．正方形ABCD在平面α的同侧，若A、B、C三点到α的距离分别为2，3，4，则BD
所在直线与平面α的位置关系是
15．设正方体
，恰好到其中5个面所在平面的距离都相等的点共有
个，平面M与各条棱所成的角都等于
，则
。
16．在体对角线长为l的长方体中，体对角线在相邻三个面内的射影长的和的最大值等于
___
三． 解答题（共74分）
17．（10分）已知四边形ABCD中，∠ABC=∠BCD=∠CDA=∠DAB=90º，求证：四边形是矩形。
18．（12分）如图，P是⊿ABC所在平面外一点，M，N分别是PA和PB的中点，试过点M，N做平行于AC的平面。要求：
（1）画出平面分别与平面ABC，平面PBC，平面PAC的交线；
|
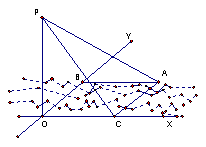
19．（12分）有一条东西方向的河流，在岸边设探照灯P，PO垂直于地面
，灯光PA射向正东北方向，且与地面成60º角，求灯光PA与河岸OX所成角的余弦。
|
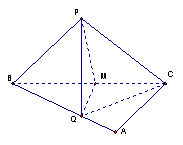
20．（10分）直角三角形ABC中，∠A=90º，AB=2AC，Q为AB上一点，QB=
AC，P为平面ABC外一点，且PB=PC，求证：PQ⊥BC。
|
21．（14分）若直线L与平面内三条两两相交的直线a,b,c所成的角相等。求证:L⊥.
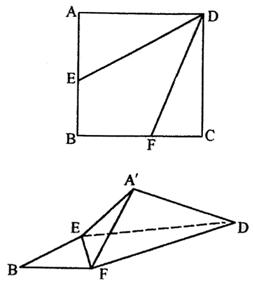
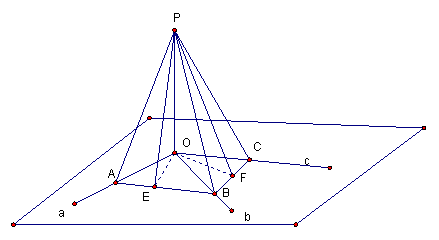
22．（16分）正方形ABCD中，AB=2，E、F分别是边AB及BC的中点，将△AED及△DCF折起（如图），使A、C点重合于
点.
（Ⅰ）证明D⊥EF；
（Ⅱ）求三棱锥—EFD的体积；
（Ⅲ）求D与平面DEF所成角的正切值.
|
参考答案
一、选择题（本题每小题5分，共60分）
BCDA ADAA BDBB
3．解：取AB=1，AD=2，
，验算即得仅D适合
7．所成角的余弦值都是
，因此所成角的弧度数只有1种，选（A）
8．解 取锐角△ABC，设其垂心为H，过H作直线k，使k与平面ABC垂直，设CP是△ABC的一条高，在l上取一点D，使△DPC是锐角三角形，并作CQ
DP，CQ与l交于E，则A、B、C、D、E这五个点中任意两点的连线与其他三点确定的平面垂直。选（A）。
10． 解 当直线a与P点确定的平面与b平行时，过P点所作的与a相交的直线都在内，不可能与b相交，因此命题①不正确；同样，在这种情况下，过P点作与b平行的平面恰是，通过a与a并不平行，因此命题②也不正确。选（D）。
12．解 因为棱锥的各侧棱与底面所成角相等，所以顶点在底面内的射影是底面四边形的外接圆圆心，底面四边形ABCD是圆内接四边形。设A：B：C=2：3：4，由于A+C=180，因此A=60，C=120，B=D=90，最小角为A=60。 选（B）。
二、填空题（本题每小题4分，共16分）：
13．平行或异面；
14．BD//；由图可知B，D两点到平面的距离都是3，故BD//。
15．解：6；
提示：正方体的中心O关于六个面的对称点均合条件，故所求的点共有6个；平面M有无数个，其中一个是平面
，恒有
16．解：解 设长方体中过同一个顶点的三条棱长分别是x，y，z，则体对角线l=
。
注意到由a2+b2
2ab，b2+c22bc，c2+a22ca可导出2（a2+b2+c2）2（ab+bc+ca）
3（a2+b2+c2）（a+b+c）2 以
代入上式，便得3[（x2+y2）+（y2+z2）+（z2+x2）] （
）2
即 6l2（
）2 ，
不等式左端即体对角线在相邻三个面上的射影的和。
三、解答题（共74分）
17．证明：若四点A，B，C，D不在同一平面内，设A点在平面BCD内的射影（垂足）为O，则AO⊥BC，又∵BC⊥AB，∴BC⊥面AOB，∴BC⊥OB；同理DC⊥OD。
但
∴
，矛盾。故四点A，B，C，D在同一平面内，即四边形ABCD是矩形。
18．解：（1）过N点作NE//AC交BC于E，过M点作MF//AC交PC于F，连结EF，则平面MNEF为平行于AC的平面，NE，EF，MF分别是平面与平面ABC，平面PBC，平面PAC的交线。
（2）∵NE//AC，MF//AC，∴NE//MF。∴直线NE与MF共面，NE，EF，MF分别是平面MNEF与平面ABC，平面PBC，平面PAC的交线。
∵NE//AC，NE
平面MNEF，∴AC//平面MNEF。∴平面MNEF为所求的平面。
19．
解：∵PO⊥平面XOY，∴∠PAO是灯光PA和地面所成的角，从而∠PAO=60º，∠AOX=45º。作AB⊥OY于B，AB//OX，故∠PAB是灯光与河岸所成的角。设PA=a,则OA=PAcos60º=
a,AB=OAsin45º=
a.在Rt⊿PBA中cos∠PAB=
20．
证明：取BC中点M，连接PM，QM，令AC=1，则BQ=，∵AB=2AC=2，∴QA=2-=
∴QC=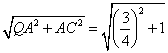
=。∴QC=QB，∴QM⊥BC。又∵PM⊥BC，∴BC⊥平面PMQ，∴BC⊥PQ。
21．证明：∵直线L与平面内的两两相交的直线a,b,c所成的角相等，∴L
，L与相交不妨设直线a,b,c都过L与平面的交点O。在a,b,c上分别A，B，C，使得OA=OB=OC。在L上取一点P，则∠POA=∠POB=∠POC，∴⊿POA≌⊿POB≌⊿POC，则PA=PB=PC。取AB，BC的中点分别为E，F，则PE⊥AB，PF⊥BC，且OE⊥AB，OF⊥BC，又∵PE∩OE=E，PF∩OF=F，∴AB⊥平面POE，BC⊥平面POF。则L⊥AB，L⊥BC而AB∩BC=B，∴L⊥。
22．证明：（Ⅰ）∵D⊥E，D⊥F，
∴D⊥平面EF，∴
D⊥EF……4分
（Ⅱ）∵D⊥平面EF ∴D的长为三棱锥
D—EF的高. E=F=1，又EF
，
∴∠EF=90°…………6分， ∴
……9分
（Ⅲ）取EF中点G，连G，DG，∵E=F=1，∠EF=90°，∴G⊥EF，得G
又∵G⊥EF，∴EF⊥平面DG，∴平面DEF⊥平面DG. ………11分 作H⊥DG于H， 得H⊥平面DEF， ∴∠DG为
D与平面DEF所成角…………14分 在Rt△DG中 
D=2 
DG
……………………16分