高二数学下学期第二次月考试题

高二数学下学期第二次月考试题

一.　 选择题(5′×12=60′)

1.有4名同学争夺3项冠军,冠军获得者共有(　 )种可能.

A.4³　　　 B.3⁴　　　　　　　 C.4×3　　　　　 D.以上都不对

2.上午有4节课,下午有2节课,安排5门不同的科目,其中有一门要求两节连上,不同的排课方式(　 )

A.96　　　　　　　　　　 B.120　　　　　　 C.480　　　　　　 D.600

3.(　 )

A.3ⁿ　　　　　　　B.　　　　　　C.　　　　　　　D.

4.已知P(A)= ,P(B)= ,则(　　)

A.P(A·B)= 　　 B. P(A·B)= 　 C. ≤ P(A·B) ≤　　　D. ≤P(A·B)≤

5.某厂大量生产某种小零件,经抽样检验知其次品率为1%,现把这种零件每6件装成一盒,那么每盒中恰含一件次品的概率为(　 )

A.　　 B.0.01　　 C.　　　　　 D.

6.=(　 )

A.-1　　　　B.1　　　　 C.-2　　　　D.2

7.(理)等差数列中,d≠0,n>200,则的值为(　 )

A.不存在　　　　　　　B.1　　　　 C.　　　　　D.以上都不对

(文)已知函数,(　 )

A.不存在　　　　　　　B.存在　　　　　 C.无法确定　　　　　 D.以上都不对

8.大,中,小三个盒子中分别装有同一种产品120个,60个,20个,现需要从这三个盒子中抽取一个容量为25的样本,较为合适的抽样方法为(　 )

A.分层抽样　　　　　 B.简单随机抽样　　　　　 C.系统抽样　　　　　 D.以上三种均可

9.(理)设随机变量,则P的值为(　　)

A.-1　　　　B.0　　　　 C.1　　　　 D.0.5

(文)在抽查某产品的尺寸过程中,将其尺寸分成若干组,[a,b]是其中一组,抽查处的个体数在该组上的频率为m,该组上的直方图的高为h,则a-b等于(　 )

A.h+m　　　 B.h-m　　　 C.　　　 D.

10.(理)函数的导数是(　 )

A.　　 B.　　　 C.　　　　D.(2x²-1)log_ae

(文)曲线处的切线的倾斜角为(　 )

A.45⁰　　　 B.225⁰　　　C.-45⁰　　　D.135⁰

11.若函数f(x)=x³-ax²+1在(0,2)内单调递减,则实数a的取值范围是(　)

A.a≥3　　　B.A=3　　　 C.a≤3　　　D.0<a<3

12.(理)给出下列4个命题:①函数y=x²-5x+4(-1≤x≤1)的最大值为10,最小值为;

②函数y=2x²-4x+1(2< x <4)的最大值为17,最小值为1;③函数y=x³-12(-3< x <3)的最大值为16,最小值为-16;④函数y=x³-12 (-2< x <-2)无最大值,无最小值.其中正确地命题(　 )

A.4个　　　 B.3个　　　 C.2个　　　 D.1个

(文)一个总体中的100个个体的编号为1,2,3,…,100,平均分在10个小组,组号分别依次为0,1,2,…,9,要用系统抽样方法抽取一个容量为10的样本.规定如果在第0小组随即抽取的号码为m,那么第k小组抽取的号码的个位数为m+k或m+k-10(如果m+k≥10),当m=7时,所抽取样本的第6个号码是(　 )

A.50　　　　B.51　　　　C.52　　　　D.53

二.　填空题(4′×4=16′)

13.三次函数f(x)= x³-3bx+3b在[1,2]内恒为正值的充要条件为(　 )

14.有n个房间,分给n个不同的人,每个人都以的概率进入每一个房间,而且每间房里得人数没有限制,那么不出现空房的概率(　　　　)

15.(　　 )

16.(理)的值为(　　 )

(文)已知曲线y=x³+3x在点P的切线与直线y=15x+3平行,则坐标为(　　　　　　　　  )

第二卷

姓名　　　　　  ,班级　　　　  　　

题号	1	2	3	4	5	6	7	8	9	10	11	12
选项

13.　　　　　　　　  ;　 14.　　　　　　　　 

15.　　　　　　　　　　　　16.　　　　　　　　 

三.　解答题(共4′)

17.(12′)已知,而等于它后一项系数的,试求该展开式中二项式系数最大的项,并求出该项.

18. (12′) (理)平面内有n条直线,其中无任何两条平行,也无任何三条共点.

求证:这n条直线把平面分割成块.

(文)甲、乙二人投篮,投中的概率分别为0.6,0.7,今各投3次,

求:甲比乙投中次数多的概率.

19. (12′)已知曲线f(x)=x³+px²+qx的图像与x轴相切于异于原点的的一点,又函数有极小值-4.

求f(x)的单调区间.

20. (12′)(理)设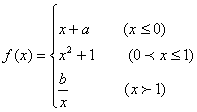,问:a、b为何值时,f(x)在定义区间内连续?

(文)某的现有耕地面积10000公顷,规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%,若人口增长率为1%,那么耕地面积平均每年至多只能减少多少公顷(精确到1.0)?

(粮食单产=,人均粮食占有量=).

21. (12′)(理)如图所示:甲、乙两个工厂,甲厂位于一条直线河岸的岸边的A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40km的B处,乙厂到河岸的垂足D与A相距50km,两厂要在此河岸边合建一个供水站C,从供水站到甲厂和两厂的水管费用为每千米3a元,5a元,问供水站C建在岸边何处才能使水管费用最省?

(文)已知f(x)=x³+bx²+cx+d在(-∞,0)上是增函数,在[0,2]上是减函数,且方程f(x)=0有三个根,它们分别是:

①　　 求c的值;②求证: f(1)≥2;③求∣∣的取值范围.

22. (14′)(理)一名学生骑自行车上学,从家到学校的途中共有6个交通岗,假设他在各个交通岗遇到红灯的概率事件相互独立,且概率都是.

①　　 设ξ为这名学生在途中遇到红灯的次数,求ξ的分布列;

②　　 设η为这名学生在首次停车前经过的路口数,求η的分布列;

③　　 求这名学生在途中至少遇到一次红灯的概率.

(文)已知两家工厂上半年每月工业生产产值如下表(单位:万元)

月份	一	二	三	四	五	六
甲厂	70	50	80	40	65	55
乙厂	55	65	55	65	55	65

试分析两厂家的生产情况.