高二数学第二学期试题

高二数学第二学期试题

（满分150，时间120分钟）

第Ⅰ卷

一．选择题（每小题5分，共60分）

1．若平面α的一条斜线l与α成60⁰角，则l与平面α内的直线所成的角（　　）

A.　　  最小为60⁰，最大为90⁰　　　　　　　　　

B.  最小为60⁰，不存在最大角

C.　　  最大为90⁰，不存在最小角　　　　　　

D.　　 不存在最小角也不存在最大角

2．若平面α∥平面β，直线l在α内，且α与β之间的距离为d，下面给出四个命题：

①　　 β内有且只有一条直线与l的距离等于d

②　　 β内所有直线与l的距离都等于d

③　　 β内有无数条直线与l的距离等于d

④　　 β内所有直线与α的距离都等于d

其中正确的的是（　　）

　A. ①　　　　　　　　　　 B. ②　　　　　　　　　　　C. ①与②　　　　　 D. ③与④

3．已知x=5⁹⁹+C5⁹⁸+C5⁹⁷+…+C，那么x被7除的余数为（　　）

　　　 A. －2　　　B.　5　　　　C. －1　　　　  D.  6

4．已知正方体ABCD-A₁B₁C₁D₁的棱长为3，E为CD的中点，则点D₁到平面AEC₁的距离为（　　）

　　 A. 　　　　　　　　　　B. 　　　　　　　　　 C. 　　　　　　　 D. 1

5．一个棱锥被平行于底面的平面所截，若截面面积与底面面积之比为1：2，则此棱锥的高被分成两段之比（自上而下）为（　　）

　　 A. 1：2　　　　　　　　　　B. 1：4　　　　　　　　　 C. 1：（+1）　D. 1：（）

6. 展开式的第四项等于7，则x等于

A. －5　　　　　　　　　　　 B. -　　　　　　　　　　　　C. 　　　　　　　　　　　　 D. 5

7．球的两个平行截面面积分别为5π和8π，球心到这两个截面的距离之差等于1，则球的直径为（　　）

　　 A. 3　　　　　　　　　　　　　B. 4　　　　　　　　　　　　C. 5　　　　　　　　　　D. 6

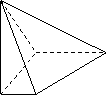
8．一个简单多面体的各面都是三角形，且有6个顶点，则此简单多面体的面数是（　　）

　　 A. 4　　　　　　　　　　　　　B. 6　　　　　　　　　　　　C. 8　　　　　　　　　　D. 10

⒐　6名学生和1名教师排成一排照象，若教师排中间，其中学生甲排在学生乙的左侧，那么不同排法有（　　）

　　　 A.  P　　　　  B.  P　　　　　C. 2P　　　　D. 4P

10．直线a是平面的斜线，b ，当a与b成60⁰的角，且b与a在内的射影成45⁰角时，a与所成的角是（　　）

　　 A. 60⁰　　　　　　　　　　　 B. 45⁰　　　　　　　　　　 C. 90⁰　　　　　　　　 D. 135⁰

11．一个正方体内接于一个球，过球心作一截面，则截面的可能图形是（　　）

①　　　　　　　　②　　　　　　　　③　　　　　　　　④

　　 A. ①③　　　　　　　　　　B. ②④　　　　　　　　　C. ①②③　　　　　 D. ②③④

12．在北纬45⁰圈上有甲、乙两地，它们的经度分别是东经140⁰与西经130⁰，设地球半径为R，则甲、乙两地的球面距离是（　　）

　　 A. 　　　　　　　　　B. 　　　　　　　　C. 　　　　　　D.

第Ⅱ卷

题号	1-12	13-16	17	18	19	20	21	22	总分
得分

一、选择题：（每小题5分，满分60分）

　　在每小题给出的四个答案中，只有一个答案是正确的，请将正确的答案选出来，将其代号填写在下表中对应的题号下.

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二．填空题（每小题4分，共16分）

13. 已知(1-3x)⁶(1-2x)⁵=a₀+a₁x+a₂x²+…+anx¹¹，则a₁+a₂+…a₁₁=_________。

14．四个半径为r的球，将它们分上、下两层垒放在桌面上，并且使它们两两相切，则最上面一个球的最高点到桌面的距离为___________

15．等边三角形ABC的边长是，AD是BC边上的高，沿AD将ΔABC折成直二面角，则点A到BC的距离__________

16．给出四个条件：

①　　 棱柱有一条侧棱和底面垂直

②　　 棱柱有一个侧面和底面一条边垂直

③　　 棱柱有一个侧面是矩形且和底面垂直

④　　 棱柱有一条侧棱和底面的两条边垂直

在以上4个条件中，棱柱成为直棱柱的一个必要而不充分条件有(填入序号)__________

三．解答题（本题有6小题，计74分）解答应写出文字说明，证明过程或演算步骤

17．（本题12分）已知P是平面四边形ABCD所在平面外一点，且AB=BC，AD=CD，PA=PC，

求证：平面PAC⊥平面PBD

18．（本题满分12分）

（1）求证：

（2）设(1－x)²⁰⁰²＝a₀＋a₁x＋a₂x²＋……＋a₂₀₀₂x²⁰⁰²，其中，a₀，a₁，a₂，…，a₂₀₀₂

是常数，求：(a₀＋a₂＋a₄+……＋a₂₀₀₂)²－(a₁＋a₃＋a₅+……＋a₂₀₀₁)² 的值.

S 　　　　 B　　　　 C 　A　　　 D

19．（本题12分）如图，ABCD是直角梯形，∠BAD=90⁰，∠SAB=90⁰，SA⊥面ABCD，SA=AB=BC=1，AD=，求面SCD与面SBA所成的二面角的正切值。

20．（本题满分12分）

一个口袋内装有4个不同的红球，6个不同的白球，若取出一个红球记2分，取出一个白球记1分. 问：从口袋中取5个球，使总分不小于7分的取法有多少种？

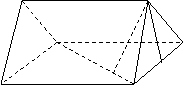
21．（本题12分）如图，直三棱柱ABC-A₁B₁C₁的侧棱AA₁=4cm，底面是等腰直角三角形，且AC=BC=2cm，∠C=90⁰，E为AB的中点，CD⊥AB₁

C1　　　　　　　　　  C 　　B1　　　　　　　　　　　　　   B 　　　　　　　　 D　　　　E A1　　　　　　　　　　 A

（1）　 求异面直线CE与AB₁的距离

（2）　 求点E到平面ACB₁的距离

22．（本题14分）设ΔABC和ΔDBC所在的两个平面互相垂直，且AB=BC=BD，

∠ABC=∠DBC=120⁰，

求：（1）直线AD与面BCD所成角的大小

A B　　　　　  C D

（2）异面直线AD与BC所成的角

（3）　　　 二面角A-BD-C的大小。