高二数学阶段性考试试题

高二数学阶段性考试试题

班级　　　　  姓名　　　　　  学号

一、选择题（每题5分，共50分）

1．某位同学一次掷出3个骰子，得到3个6点的事件为 （　C　）
A．不可能事件　 B.必然事件　C.随机事件　D.无法确定

2．下列说法正确的是 ( D　 )
A．某厂一批产品的次品率为0.1，则任意抽取其中10件产品一定会发现一件次品
B．气象部门预报明天下雨的概率是90﹪，说明明天该地区90﹪的地方要下雨，其余10﹪的地方不会下雨
C．某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈
D．掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0.5．

3．从1，2，…，9这九个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是（C）

A.　　  B.　　  C.　　D.

4．已知p：则p是q的（ A　 ）

　　　 A．充分不必要条件 B．必要不充分条件

　　　 C．充要条件 D．既不充分也不必要条件

5．设变量、满足约束条件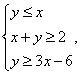则目标函数的最小值为（B）

　　　 （A）2　　　　（B）3　　　　（C）4　　　　（D）9

6．下列结论正确的是（B）　　　　　　　　　　　　　　

　　　 A．当　　　　　 B．

　　　 C．的最小值为2　　　　　 D．当无最大值

7．设，则下列不等式成立的是　　　 （B）

　　　 A．　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　 D．

8．函数图象上最低点的坐标为　　（ B ）

（A）（0，5）　　(B) （3，4）　 (C) （3，2）　　(D) （8，）

9．若不等式x²＋ax＋1³0对于一切xÎ（0，）成立，则实数a的最小值为（ C ）

A．0　　 B. –2　　C.-　　  D.-3

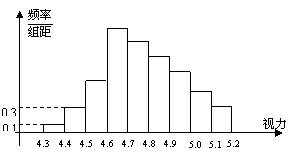10．为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，如右，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a, b的值分别为（　 A ）

　　　 A．0,27,78　　　　　　　 B．0,27,83

　　　 C．2.7,78　　　　　　　　 D．2.7,83

–2　　 C.-　　  D.-3

a←0 j←1 While　j≤5 a←mod(a+j, 5) j←j+1 End　While Print　a，j End

二、选择题（每题5分共30分）

11．不等式的解集是　　 .

12．右边伪代码运行输出结果为___0，6______________。　　　

13．函数的值域为（）。

14．某公司一年购买某种货物400吨，每次都购买吨，运费为

4万元/次，一年的总存储费用为万元，要使一年的总运费与总

存储费用之和最小，则（ 20 ）吨。

15．一组数据中的每一个数据都减去80,得到一组新数据的平均值是1.2,方差是4.4,则原数据的平均值和方差分别是　 (81.2　 ， 4.4 )。

16．对任意实数a，b，c，给出下列命题：①“”是“”充要条件；②“是无理数”是“a是无理数”的充要条件③“a>b”是“a²>b²”的充分不必要条件；④“a<5”是“a<3”的必要不充分条件。

其中真命题的序号是______②_____④_________。

三、解答题

17．（本题满分14分）

（1）袋中有2个红球,2个白球,2个黑球,从中任意摸出2个球，求至少有1个红球的概率。

（2）用计算机随机产生的有序数组（x, y），满足-1 < x <1, -1 < y < 1，求数组（x, y）满足 x - y > 0 的概率。

答案：

18．（本题满分14分）设函数

（1）若不等式的解集为R，求实数m的取值范围。

（2）若不等式有解，求实数m的取值范围。

答案：

19．1,1,2,3,5,8,13，这一数列的规律是：第1、第2个数是1，从第3个数起，该数是前面2个数的和。试用伪代码写出计算这个数列前30项和的算法，并画出流程图。

20．甲、乙两地相距s千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米/时．已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成：可变部分与速度v(千米/时)的平方成正比，且比例系数为b；固定部分为a元．

(Ⅰ)把全程运输成本y(元)表示为速度v(千米/时)的函数，并指出这个函数的定义域；

(Ⅱ)为了使全程运输成本最小，汽车应以多大速度行驶？

答案：（1）,（2）当时，，当时，

21．已知，函数

（1）当时，若对任意都有

（2）当时，证明：对任意

（3）当探讨：对的充要条件（不必证明）。

（答案0<a<1）