高二数学期末复习题精选
（一）圆锥曲线
班级____________姓名______________ 学号____________
一、选择题（共20小题，每小题3分，共60分）
1、设q是第四象限角，则方程x2sinq＋y2=sin2q表示的曲线是 ( )
(A)焦点在x轴上的椭圆 (B)焦点在y轴上的椭圆
(C)焦点在x轴上的双曲线 (D)焦点在y轴上的双曲线
2、过点(
，0)的直线与直线x-y-1=0的交点在圆x2＋y2=1上，则这条直线的斜率为( )
(A)-2 (B)-2或0 (C)2 (D)0或2
3、焦点为（1，1），准线为x =3的抛物线方程为 ( )
(A)(y－1)2=－4(x－2) (B)(y－1)2=－2(x－2)
(C)(y－1)2 = 4(x－2) (D)(y－1)2 = 2(x－2)
4、方程2x2-3y2-8x＋18y-19=0所表示的曲线是 ( )
(A)椭圆 (B)双曲线
(C)二条相交直线 (D)二条平行线
5、直线ax－y＋1=0与x－ay－1=0的交点轨迹方程是 ( )
（A）y=x或x－y＋1=0 （B）x－y＋1=0
（C）x－y=0或x＋y－1=0 （D）x＋y－1=0
6、椭圆的一个焦点到长轴的两个端点的距离的比为2∶3，则离心率为 ( )
(A)
(B)
(C)
(D)
7、如果A是B的必要条件，B是C的充要条件,D是C的充分条件，则D是A的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)不充分也不必要条件
8、设F1、F2为双曲线
-y2=1的两个焦点，点P在双曲线上且满足
F1PF2=900，则ΔF1PF2的面积是
( )
(A)1
(B)
/2
(C)2
(D)
9、圆C1：x2＋y2－2x－6y＋9=0关于直线x－y－1=0对称的曲线方程为( )
(A)x2＋y2＋2x＋6y＋9=0 (B)x2＋y2－6x－2y＋9=0
(C)x2＋y2－8x＋15=0 (D)x2＋y2－8x－15=0
10、以方程x2-96x+1=0的二根分别为离心率的曲线可为 ( )
(A)两个椭圆 (B)一椭圆的一双曲线
(C)一椭圆和一抛物线 (D)一双曲线和一抛物线
11、圆心在抛物线y2=2x上，且与x轴和该抛物线的准线都相切的一个圆的方程是
( )
(A)x2＋y2-x-2y-
=0
(B)x2＋y2＋x-2y＋1=0
(C)x2＋y2-x-2y＋1=0
(D)x2＋y2-x-2y＋=0
12、曲线x2＋4y2=13和x2＋y2=7的交点的个数是 ( )
(A)1 (B)2 (C)3 (D)4
13、双曲线4x2+my2=4m的虚轴长是 ( )
(A)2m
(B)-2m
(C)2
(D)2
14、双曲线(6x)2-(8y)2=482上一点P到它右焦点的距离是8，则P到右准线的距离是
( )
(A)
(B)
(C)2
(D)10
15、过点(
，5)与双曲线
有且只有一个公共点的直线有
( )
(A)一条 (B)二条 (C)三条 (D)四条
16、椭圆
(x＋2)2＋y2=1与抛物线y=1－(x＋1)2交点个数是
( )
(A)0 (B)1 (C)2 (D)3
17、条件
是
的
( )
(A)充分但不必要条件 (B)必要但不充分条件
(C)充要条件 (D)既不充分又不必要条件
翰林汇
18、椭圆
上一点P,它到左准线的距离为2.5,那么点P到右焦点的距离与到左焦点的距离之比是
( )
(A)3：1 (B)4：1 (C)15：2 (D)5：1
19、抛物线x2-10x-4y＋21=0的准线方程是 ( )
(A)x=4 (B)x=-4 (C)y=-2 (D)y=0
20、已知定点A(0，0),B(4，0)的动点P，
(1)当动点P满足条件：
时所得的轨迹曲线为C1
(2)当动点P满足条件：PA⊥PB时所得的轨迹曲线为C2
(3)当动点P到线段A、B的中点的距离等于2时所得的轨迹为曲线C3
(4)当动点P和A、B组成以AB为斜边的直角三角形ABC时，动点P的轨迹为曲线C4
其中正确的是 ( )
(A)曲线C1、C2、C3、C4都是相同的 (B)仅有曲线C1、C2、C3是相同的
(C)曲线C1和C3相同、C4和C2相同 (D)仅有曲线C2、C3、C4是相同的
二、填空题
1、已知椭圆的两个焦点是F1(0，-1)和F2(0，3)，且点(2，1)在椭圆上，则这个椭圆方程是 。
2、若将曲线f(x,y)=0平移(沿水平或竖直方向)后, 使曲线上点P的坐标由(1,0)变为(2,2), 则平移后的曲线方程为____________.
3、曲线2y2＋3x＋3=0与曲线x2＋y2-4x-5=0的交点的坐标为__________。
4、双曲线离心率为2，则渐近线夹角为________。
5、已知抛物线x2-ay-4=0与圆x2＋y2=8有三个交点，则a=_____。
6、离心率
，焦点为F1（1，2）、F2（5，2）的椭圆方程是________
7、正三角形的两个顶点在抛物线y2=2px上，另一个顶点在原点，则这个三角形的边长等于＿＿＿＿。
翰林汇
8、双曲线的离心率为e，它的共轭双曲线的离心率为＿＿＿。
9、已知动点P满足
，A(0，-5)，B(0，5)，则点P的轨迹方程为______。
10、方程ax2＋bx＋c=0无实根，则双曲线
的离心率的范围是_______。
11、经过点(1，2)的直线与双曲线y=
相交于A、B两点，线段AB中点的纵坐标为
，则a的取值范围是__________。
12、双曲线的一条准线的与渐进线的交点为A、B，相应焦点为F，如果△ABF是正三角形，则双曲线的离心率为＿＿＿＿＿＿＿。
13、若等腰三角形底边的两个端点是A(4,2)和B(-2,0), 则顶点C的轨迹方程是＿＿＿＿＿。
14、双曲线的渐近线方程为y
，则此双曲线的离心率等于＿＿＿＿＿。
15、双曲线
的离心率
则m的取值范围是＿＿＿＿。
16、椭圆
上的点，直线x＋2y-5
=0的最小距离是______________。
17、直线y=kx-1和圆(x+1)2+(y-1)2=4相离，则k的取值范围是＿＿＿＿。
18、已知P是双曲线
上一点，F1，F2是双曲线两个焦点，且
F1PF2的面积为
，则ÐF1PF2的大小是
。
19、一椭圆是由底面直径为12的圆柱被与底面成30°角的平面所截而得，则此椭圆的离成心率为＿＿＿。
20、(1)已知x2＋4y2=4x，点P(x0，y0)在这个方程的曲线上，当
取得最大值时，点P的坐标是
。
(2)如果圆锥曲线
=1的离心率等于2，那么m的值是 。
(3)已知椭圆
上一点P到左右两焦点距离之比为1∶4.则点P到它的左右两条准线的距离分别为
。
三、解答题
1、已知抛物线y2=32x的焦点是F，若以F和另一定点F’(8，8)为焦点作与抛物线相交的椭圆，求长轴最短的椭圆的方程。
翰林汇
2、如果抛物线y2=ax(a为参数)与圆(x－2)2＋y2=3相交，连接在x轴同侧的两个交点的线段，求线段中点的轨迹。
翰林汇
3、已知抛物线x2=4y与圆x2＋y2=32相交于A、B两点，圆与y轴正向交于点C，
是过ACB弧上的点且与圆相切，与抛物线相交于M、N两点的直线，d是M、N两点到抛物线焦点的距离之和。求：(1)A、B、C三点的坐标；(2)当d取最大值时C的方程。
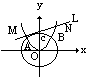
翰林汇
4、AB是过双曲线3x2-y2+24x+2y+44=0右焦点的弦,且
等于双曲线的焦距,试求直线AB的方程.
翰林汇
5、已知双曲线的两渐近线方程为3x-4y=2和3x+4y=10,一条准线方程为5y+4=0,求此双曲线的方程.
翰林汇