高二年级上学期数学周末练习
第Ⅰ卷
一；选择题（每小题5分，共计60分）
【注意】请把选择题答案填写在答题卡上！
1．设
、
表示两条直线，
、
表示两个平面，下列命题中真命题是
Ａ、若
，∥，则∥． Ｂ、若，∥，则∥．
Ｃ、若∥，⊥，则⊥． D、若∥，⊥，则⊥．
2．在棱长为
的正方体ABCD－A1B的棱共有
A、2条 B、3条 C、4条 D、5条
3．正四棱锥P—ABCD的侧面PAB为等边三角形，E是PC的中点，是异面直线BE与PA所成角的余弦值为
A、
B、
C、
D、
4．已知二面角—l—
的大小为
，两异面直线
、
，⊥，⊥，则、所成角等于
A、
B、
C、
D、或
5．若斜线l与平面
所成角为，在内任作l的异面直线，则l与所成的角有
A、最大值
，最小值
B、最大值
，最小值
C、最大值
，最小值
D、不存在最大值和最小值
6．E，F分别是三棱柱ABC－A1B
A、
B、
C、
D、
7．平行六面体的棱长都为，从一个顶点出发的三条棱两两都成600角，则该平行六面体的体积为
A、
B、
C、
D、
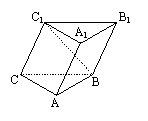8．如图，在斜三棱柱A1B
A、直线AB上 B、直线BC上
C、直线AC上 D、△ABC内部
9．在下列条件中,可判断平面与平行的是
A、、都垂直于平面
B、内存在不共线的三点到的距离相等
C、
、是内两条直线,且∥,∥
D、,是两条异面直线,且∥,∥,∥,∥
10．设地球半径为R，在北纬300圈上有甲、乙两地，它们的经度差为1200，那么这两地间的纬线之长为
A、
B、
C、
D、
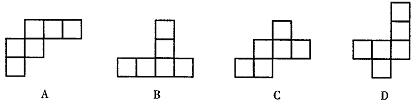
11．如图下列四个平面形中，每个小四边形皆为正方形，其中可以沿两个正方形的相邻边折叠围成一个立方体的图形是
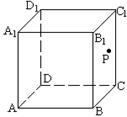12．如图, 在正方体ABCD—A1B
A、 直线 B、 椭圆 C.、 双曲线 D、 抛物线
高二数学周末练习
第Ⅱ卷
一：选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二：填空题（每小题4分，共计16分）
13．长方体的三条棱长、、c成等差数列，对角线长为
，表面积
为22，则该长方体的体积＝ 。
14．已知正四棱锥P－ABCD的高为4，侧棱与底面所成的角为600，则该正四棱锥的侧面积是 ．
15．三棱锥P－ABC的四个顶点在同一球面上, 若PA⊥底面ABC，底面ABC是直角三角形，PA＝２，AC＝BC＝１，则此球的表面积为
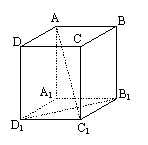16．如图，四棱柱ABCD－A1B
①四棱柱ABCD－A1B
②底面ABCD为菱形；
③AC1⊥B1D1．
以其中两个论断作为条件，余下的一个论断作为结论，
可以得到三个命题，其中正确命题的个数为 ．
三：解答题（共计74分）
17．（本题10分）已知PA垂直于矩形ABCD所在平面，M、N分别是AB、PC的中点
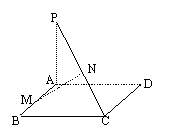求证：MN⊥AB
18．（本题12分）在四棱锥P－ABCD中，底面ABCD是矩形，AB＝，
AD＝
，PA⊥平面ABCD，PA＝
，Q为PA的中点
（1）求Q到BD的距离；
（2）求P到平面BQD的距离。
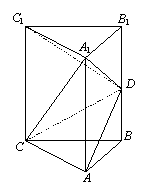19．（本题12分）如图，直三棱柱ABC－A1B
AA1，
∠BAC＝900，D为棱BB1的中点．
| |
（2）求证：平面A1DC⊥平面ADC．
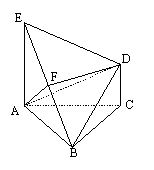20．（本题13分）如图，△ABC中，AC＝BC，AE和CD都垂直于平面ABC，且AE＝AB＝2，F为BE的中点，DF∥平面ABC，
（1）求CD的长；
（2）求证：AF⊥BD；
（3）求平面EDB与平面ABC所成的二面角的大小．
21．（本题13分）如图，将长
，宽AA1＝3的矩形沿长的三等分线处折迭成一个三棱柱，如图所示：
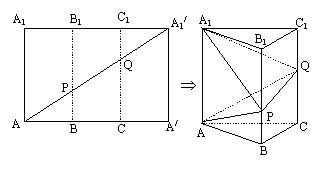(1)求平面APQ与底面ABC所成二面角的正切值；
(2)求三棱锥A1－APQ的体积.
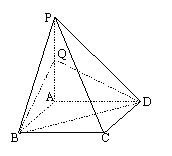
22．（本题14分）如图,四棱锥P—ABCD的底面ABCD为正方形，PD⊥底面ABCD，PD=AD.
（1）求证：平面PAC⊥平面PBD；
（2）求PC与平面PBD所成的角；
（3）在线段PB上是否存在一点E，
使得PC⊥平面ADE？若存在，请加
以证明，并求此时二面角A—ED—B
的大小；若不存在，请说明理由。