高二年级数学周末练习参考答案及评分标准
一：选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | B | D | A | B | C | A | D | A | C | B |
二：填空题（每小题4分，共计16分）
13. 6体积单位； 14. 
面积单位 15. 
16. 2个
三：解答题（共计74分
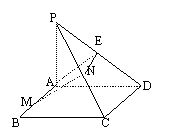
【第17题答案】：
|
…………证出四边形MNEA为平行四边形
|
|
∴AB⊥MN
说明：其他证法适当给分。
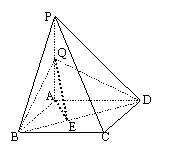
【第18题答案】
（1）作AE⊥BD于E，连接QE
………………证出QE⊥BD,
|
|
|
（2）证明：BA⊥平面PAC
|
|
【第19题答案】：
（1）连结AC1交A
|
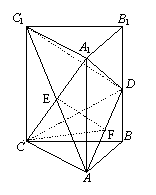设
，
则
，
．
．
中，
，
，
直三棱柱中，
，则
．
．
|
，
|
异面直线
与
所成的角为
．
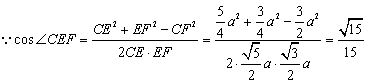（2）直三棱柱中，，
平面
．
|
．
又
，
，
，
|
， 
于是
．
A1D⊥
| |
． 又
平面
，
|
平面
平面
．
【第20题答案】：
（1）
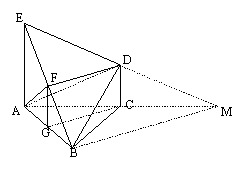取AB中点G，连FG、CG，则FG∥AE，
又∵AE和CD都垂直于平面ABC，
∴AE∥CD，∴ FG∥CD，
∴F、G、C、D四点共面．
|
|
|
．
（2）直角三角形ABE中，AE＝AB，F是BE的中点，
∴AF⊥BE，
又∵△ABC中，AC＝BC，G是AB中点，∴CG⊥AB，
又∵AE垂直于平面ABC，
∴AE⊥CG，又AE∩AB＝A，∴CG⊥面ABE．
∵DF∥CG，∴DF⊥面ABE，∴AF⊥DF，
又∵BE∩DF＝F，
|
|
……………………证明出∠ABM＝900
|
在三角形EBA中：∠EAB＝450
|
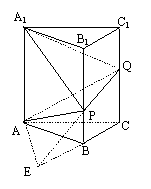
【第21题答案】：
|
三棱柱ABC－A1B
且侧棱AA1＝3，底面边长为
，
延长QP交BC延长线于点E，连AE
在△ACE中， 
，
，∠ACE=60°，于是AE=3
在△QCE中：PB∥QC, BP=1，CQ=2
|
∴AB=BC=BE ∴EA⊥AC
∵QC⊥平面ABC,AC为QA在平面ABC内的射影
|
∴∠QCA为二面角Q－EA－C的平面角
在RT△QCA中：
∠QCA＝
即：平面APQ与面ABC所成锐二面角的正切值为
…………7分
（Ⅱ）连
， 
的面积为
……………………8分
点Q到平面
的距离为 
……………………10分
∴
………………13分
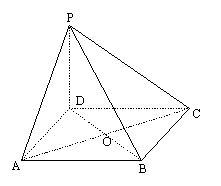【第22题答案】：
(1)∵PD⊥底面ABCD，
∴AC⊥PD，
又∵底面ABCD为正方形，
∴AC⊥BD，而PD与BD交于点D，
|
|
平面PAC，
∴平面PAC⊥平面PBD.
（2）记AC与BD相交于O，连结PO，由（1）知，
AC⊥平面PBD，
∴PC在平面PBD内的射影是PO，
|
∵PD=AD,
∴在Rt△PDC中，PC=
CD，
而在正方形ABCD中，OC=
AC=
CD，
|
即PC与平面PBD所成的角为30°.
（3）在平面PBD内作DE⊥PO交PB于点E，连AE，
则PC⊥平面ADE.以下证明：
由（1）知，AC⊥平面PBD，
∴AC⊥DE，
又PO、AC交于点O，
∴DE⊥平面PAC，
∴DE⊥PC，（或用三垂线定理证明）
而PD⊥平面ABCD，∴PD⊥AD，
又∵AD⊥CD，∴AD⊥平面PCD，∴AD⊥PC，
∴PC⊥平面ADE，由AC⊥平面PBD，
∴过点O作OF⊥DE于F，
连AF，由三垂线定理可得，AF⊥DE，
|
设PD=AD=a，在Rt△PDC中，
求OF=
a,而AO=a,
|
即所求的二面角A—ED—B为60°.