高二年下学期数学期中试卷参考答案
一. 选择题（本题共36 分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | A | A | B | D | C | B | D | D | A | C |
二、填空题（本题共16分）
13.
14.
15.
16.④
三、解答题（本题共48分）
17.解：
（1）依题意知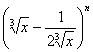
展开式中的第
项为
………………
∴前三项系数的绝对值为：
即
………
依题意知，
……………………
∴
…………………………………………………
（2）由（1）知
，令
得
……
∴第五项
为常数项……………………………
（3）令
得各项系数和为
…………………………
18.解：
分别记“甲、乙、丙参加入学考试，考试合格”为事件A、B、C则A、B、C彼此独立，并且
………………………（1）“三个人中恰有两人合格”包括三种情况：
且它们彼此互斥……………………………………………
故“三个人中恰有两人合格”的概率为：
………
……………………………………………………………………………
（2）法一：
“三人无一人合格”的概率为
……………………
又“三人无一人合格”是“三人中至少有一个合格”的对立事件……………
故“三人中至少有一人合格”的概率为
…………
法二：“三人中至少有一人合格”包括七种情况：
……………………………
“三人中至少有一人合格”的概率为：
…………………
……………………………………………………………………………
19.解：
孩子一对基因可能为
其概率分别为
，…………
孩子有显性决定特征的有
或
………………………………………
（1）1个孩子有显性决定特征的概率为
……………………
（2）2个孩子中至少有一个有显性决定特征的概率为：
…………
另解：
……………………
20.证明：
（1）∵
∴
………………………………
又
∴
……………………………………………………………
∴
…………………………………………
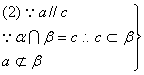21.解：（1）在长方体ABCD—A1B1C1D1中，
∴
为
与
的公垂线段…………
在
中，
∴与的距离为
…………………………………………
（2）连结AC、BD交于点O，取DD1中点O1，连结O O1∵O为BD中点
∴O O1∥BD1又A1C1//AC
∴∠AOO1（或其补角）为BD1和A1C1所成的角。………………
在
中，
∴
连结
，在
中，
……
又
∴
从而
………
在
中，
……………
∴BD1和A1C1所成的角的余弦值为
22.证明：
（1）连结
，在正方体ABCD—A1B1C1D1中，
∵
∴
∴
………………………………………………………
又
∴
又
………………
∴
……………………………………………
（2）∵
∴
（三垂线定理）…………………………………
同理可证
……………………………………………
又
∴
………………………………………………
又
∴
…………………………………………………