高二数学摸底考试试题
第I卷(60分)
一、选择题(本大题共12小题,每小题5分,共计60分,
把答案涂在答题卡上)
1. 直线3x + y - 7 = 0的倾斜角为( )
A. arctg3 B. arctg(-3)
C. π-arctg3 D.2π+arctg(-3)
2. 直线-![]() x +
x +![]() y = 1在x,y轴上的截距分别为( )
y = 1在x,y轴上的截距分别为( )
A. 3和4 B. - 3和
3. 若直线y = kx + b与x轴的负半轴相交,则有( )
A. kb> 0 B. kb<
4. 点A(a,b)关于x+y=0的对称点的坐标是( )
A. (a,-b) B. (b,a) C. (-a,-b) D. (-b,-a)
5.
当θ是第四象限时,两直线![]() 和
和
![]() 的位置关系是( )
的位置关系是( )
A. 平行 B. 垂直 C. 相交但不垂直 D. 重合
6、异于原点O的两点A , B的坐标分别为( x1 , y1 )、( x2 , y2 ),
则“![]() ”是“OA⊥OB”的( )
”是“OA⊥OB”的( )
A.必要条件 B.充分条件
C.充要条件 D.既不充分与不必要条件
7、已知直线l1:x-2y+6=0,l2:2x-y+1=0,
则l2到l1的角等于( )
A. arctg( -![]() ) B. arctg
) B. arctg![]() C. p-arctg
C. p-arctg![]() D.
D. ![]()
8.不论a为任何实数,直线(a+1)x+(
A.(-1,2) B.(-3,![]() ) C.(-2,1) D.(-1,-1)
) C.(-2,1) D.(-1,-1)
9. 设直线: 2x+y=1与直线: a2x+2y=a没有公共点,
则a的值是( )
A. –2 B.
10、过点P(4,-1),且倾斜角为直线y=2x的倾斜角的
2倍的直线方程是( )
A.4x-y-17=0 B.3x+4y-8=0
C.4x-3y-19=0 D.4x+3y-13=0
11. 已知l1与l2两条直线关于直线y=x对称,
l1: ![]() , l2: y=kx+b那么k与b的积等于( )
, l2: y=kx+b那么k与b的积等于( )
A.
15 B.
30 C.
45 D.
60
12. 把直线x - 2 y = 3沿y轴向下平移2个单位,再沿x轴
向右平移5个单位,所得直线方程( )
A. x - 2 y - 12 = 0 B. x - 2 y - 2 = 0
C. x - 2 y - 4 = 0 D. x - 2 y + 4 = 0
|
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――― 密 封 线 内 不 准 答 题
|
高二数学摸底考试试卷
第II卷(90分)
| 选择 | 填空 | 17题 | 18题 | 19题 | 20题 | 21题 | 22题 | 总分 |
二、填空题(本大题共有4小题,每小题4分,共计16分)
|
4 L 2 O 2 4 x |
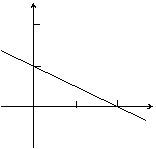
13. 如图所示直线L,对于直线上的点
(x,y),当x的值从0变到5时,
则y的值从______变到_____
14. 一条直线l过定点P(1,2), 且与
点M(4,-8)和点Q(2,0)距离相等,
则l的方程是___________
15、已知直线的倾斜角为q=arccos![]() ,且过点( 0 , 2 ),
,且过点( 0 , 2 ),
则此直线的点斜式方程为____________。
16、有下列命题:
① 过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)来表示;
② 经过不同两点P1(x1,y1)、P2(x2,y2)的直线都可以用方程
(y-y1)(x2-x1)=(x-x1)(y2-y1)来表示;
③ 经过定点A(0,b)的直线都可以用方程y=kx+b来表示;
④ 不经过原点的直线都可以用方程![]() 来表示;
来表示;
把你认为正确的所有命题的代号填上: .
三、解答题(本大题共6小题,共计76分)
17.(12分)
求倾斜角是45°,并且与原点的距离是5的直线的方程.
18.(12分)
试在直线l:x-y+1=0上找一点M,使点M到两点A(1,0)、B(3,0)的
距离和最小,求出此时点M的坐标。
19、(12分)
已知直线L经过点M( 2 , 3 ),且在两坐标轴上的截距相等,
求直线L的方程。
20.(12分)
在线性约束条件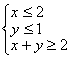 下,试求目标函数
下,试求目标函数![]() 的最大值。
的最大值。
21、(14分)
已知![]() ABC的三个顶点A(4,1)、B(7,5)、C(-4,7),
ABC的三个顶点A(4,1)、B(7,5)、C(-4,7),
(1) 求BC边上的中线所在直线的方程;
(2) 求BC边上高线所在直线的方程;
(3)求∠A的内角平分线所在直线的方程。
22.(12分)已知:△ABC的顶点A(3,-1),∠B的平分线BD所在的
直线方程为x-4y+10=0,边AB上的中线CM所在的直线方程
为6x+10y-59=0,
试求:(1)点B的坐标;
(2)边BC所在直线的方程。
参考答案:
一.CBADB BCCAD DA
二.13. 2;-![]()
14.3x+y-5=0或4x+y-6=0
15.y-2=2![]() (x-0)
(x-0)
16.②
三.17.因直线斜率为tan450=1,可设直线方程y=x+b, 3分
化为一般式x-y+b=0 5分
由直线与原点距离是5,得
![]() 8分
8分
![]() 10分
10分
所以直线方程为x-y+5![]() =0,或x-y-5
=0,或x-y-5![]() =0 12分
=0 12分
18.作A(1,0)关于直线L的对称点A’,过A’、B的直线与L交于M,
|
A’ M A B x |
则点M为所求的点。 2分
设A’(m,n),因为AA’关于L对称
所以AA’垂直于L,
且AA’中点在L上,故
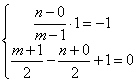 得A’(-1,2)。 6分
得A’(-1,2)。 6分
所以A’B的方程x+2y-3=0 9分
解![]() 得M(
得M(![]() ) 12分
) 12分
19.设截距为a
若a=0,则直线过O(0,0), 3分
直线方程为![]() ,即3x-2y=0 5分
,即3x-2y=0 5分
若![]() ,可设截距式方程
,可设截距式方程![]() 8分
8分
因为直线过点M(2,3)
有![]() ,得a=5,
,得a=5,
此时直线方程为x+y-5=0 10分
综上,所求直线为3x-2y=0,x+y-5=0 12分
20.画出可行域:阴影区域如图, 6分
|
L1 A L2 O B x |
作直线L: 2x-y=0
当L向右平移时,直线纵截距将变小,
当直线平移到L2位置时直,线过可行域内一点B,直线截距-Z的值最小,从而Z的值最大。 9分
由于B(2,0),故最优解为(2,0)
所以Zmax=2×2+0=4。 12分
21.(1)设BC边上的中线为AD
因为B(7,5) C(-4,7)
中点D(3/2,6), 且A(4,1)
所以中线AD所在直线方程:2x+y-9=0 4分
(2)设BC边上的高线为AE
因为BC边斜率为kBC=-2/11,所以高线AE斜率为11/2,
又A(4,1),由点斜式可得AE方程:
11x-2y-42=0 8分
(3)设A的平分线为AF,其斜率为k
易知kABkAC=-1,所以∠BAC=900, 10分
从而∠BAF=450,即AB到AF的角为450,由到角公式得
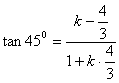 ,解得k=-7
,解得k=-7
所以AF的方程y-1=-7(x-4)即7x+y-27=0 14分
22.(1)设B(x1,y1),因为点B在BD上,所以x1-4y1+10=0 ① 2分
因为AB中点M![]() 在直线CM上
在直线CM上
所以![]() ② 4分
② 4分
解由①、②组成的方程组,得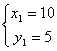 ,所以B(10,5) 6分
,所以B(10,5) 6分
(2)![]() BD平分
BD平分![]()
![]() A关于直线BD的对称点A’(m,n)在BC上
A关于直线BD的对称点A’(m,n)在BC上
故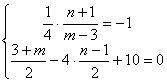 10分
10分
解得m=1,n=7,所以A’(1,7)
又B(10,5),所以可得直线BC也即BA’的方程
2x+9y-65=0 12分
 y
y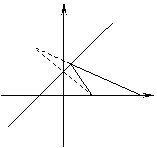 y
y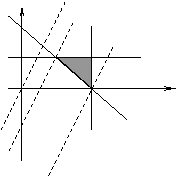 y L
y L