高二上学期第一次月考数学试题
考生注意:交卷时只交第二张试卷
一、选择题(每小题5分,共60分)
1.
设![]() ,且
,且![]() ,则必有:
,则必有:
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2. ![]() 是定义在
是定义在![]() 上单调递减的奇函数,当
上单调递减的奇函数,当![]() 时,
时,![]() 的取值范围是:
的取值范围是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.
直线![]() 的倾斜角范围是:
的倾斜角范围是:
A.![]()
![]()
![]() B.
B.![]()
C.![]() D.
D.![]()
4.
过点![]() ,且在两坐标轴上的截距相等的直线方程是:
,且在两坐标轴上的截距相等的直线方程是:
A.![]() B.
B.![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
5.
“直线![]() 直线”是“直线
直线”是“直线![]() 的斜率
的斜率![]() 等于
等于![]() 的斜率
的斜率![]() ”的:
”的:
A. 充分不必要条件 B.必要不充分条件
C. 充要条件 D.既不充分又不必要条件
6.
已知直线![]() 与
与![]() 的夹角的平分线为
的夹角的平分线为![]() ,如果
,如果![]() 的方程是
的方程是![]() ,那么
,那么![]() 的方程是:
的方程是:
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.
一直线![]() 过点
过点![]() 其倾斜角等于直线
其倾斜角等于直线![]() 的倾斜角的2倍,则直线的方程等于:
的倾斜角的2倍,则直线的方程等于:
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.
“![]() ”是“两直线
”是“两直线![]() 和
和![]() 互相垂直”的:
互相垂直”的:
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
9.
直线![]() 过点
过点![]() ,且
,且![]() 到
到![]() 的距离相等,则直线
的距离相等,则直线![]() 的方程是:
的方程是:
A.![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
10.
一批长
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
11.
方程![]() 表示的图形为:
表示的图形为:
A.两条直线 B.一条直线和一条射线 C.一个点 D.两条射线
12.
已知两点![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() 且与线段
且与线段![]() 的延长线相交,则直线的斜率的取值范围是:
的延长线相交,则直线的斜率的取值范围是:
A.![]() 或
或![]() B.
B.![]()
C.![]() D.
D.![]()
![]()
二、填空题(每小题4分,共16分)
13. 已知![]() ,
,![]() 的面积为10,则动点C的轨迹方程为 .
的面积为10,则动点C的轨迹方程为 .
14. 已知![]() 及
及![]() ,则
,则![]() .
.
15. 已知直线![]() 的方程为
的方程为![]() ,过点
,过点![]() 且与
且与![]() 垂直的直线方程为 .
垂直的直线方程为 .
16. 在抛物线![]() 上一点P,使得P到直线
上一点P,使得P到直线![]() 的距离最短,则点P的坐标为 .
的距离最短,则点P的坐标为 .
三、计算题(本大题有6小题,共74分)
17.(本题12分) 经过点![]() 的光线射到
的光线射到![]() 轴上,反射后经过点
轴上,反射后经过点![]() ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.
18. (本题12分) 直线![]() 在
在![]() 轴上的截距是1,并且
轴上的截距是1,并且![]() 到直线
到直线![]() 的角为
的角为![]() ,求
,求![]() 的方程.
的方程.
19. (本题12分) 已知直线![]() 被两条直线
被两条直线![]() 和
和![]() 截得的线段的中点恰好是坐标原点,求直线
截得的线段的中点恰好是坐标原点,求直线![]() 的方程.
的方程.
20. (本题12分) 已知直线![]() 过点
过点![]() ,且被两平行直线
,且被两平行直线![]() 与
与![]() 截得的线段长为
截得的线段长为![]() ,求直线
,求直线![]() 的方程.
的方程.
21. (本题12分) 已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地,东车站每年最多运280万吨煤,西车站每年最多运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.煤矿应怎样编制调运方案,使总运费最少?
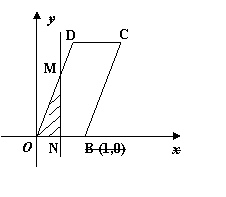 22. (本题14分) 如图, 已知
22. (本题14分) 如图, 已知![]() 是平行四边形,
是平行四边形,![]() 动直线
动直线![]() 由
由![]() 轴起向右平移,分别交平行四边形两边与不同的两点
轴起向右平移,分别交平行四边形两边与不同的两点![]() .(1)求点
.(1)求点![]() 和
和![]() 的坐标,写出
的坐标,写出![]() 的面积关于
的面积关于![]() 的表达式
的表达式![]() ;(2)当
;(2)当![]() 为何值时,
为何值时,![]() 有最大值,并求最大值.
有最大值,并求最大值.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | A | D | B | C | D | A | B | A | B | B | B | B |
13. ![]() 14.
14. ![]() 15.
15. ![]()
16. ![]()
17. 解:作A(1,2)点关于y轴的对称点 N(-1,2) 则NB所在的直线即为反射光线所在直线,
由两点式,得 ![]()
18. 解:设所求直线方程为![]() 又
又![]() 由到角公式得
由到角公式得
![]() 所以
所以 ![]()
![]() 故所求的方程为:
故所求的方程为:![]()
19.解:方法一:当直线![]() 的斜率
的斜率![]() 存在时,设
存在时,设![]() 的方程为
的方程为![]() ,且
,且![]() 与已知两直线的交点分别为
与已知两直线的交点分别为![]() ,
,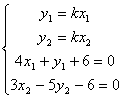 解得
解得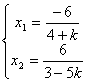
![]() 是
是![]() 的中点,
的中点,![]() .
.
即![]() 解之,得
解之,得![]() .
.
当斜率![]() 不存在时,直线
不存在时,直线![]() 是
是![]() 轴,它和两已知直线的交点分别是
轴,它和两已知直线的交点分别是![]() 和
和![]() ,显然不满足中点是原点的条件,所求的直线方程为
,显然不满足中点是原点的条件,所求的直线方程为![]() .
.
方法二:设过原点的直线交已知两条直线于A、B,且O为A、B的中点,
所以 A与B关于原点对称.
若设![]() ,
,
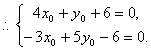 解之得
解之得![]()
所以点![]() 都满足方程
都满足方程![]() ,
,
![]() 过两点的直线有且只有一条,该直线过原点,
过两点的直线有且只有一条,该直线过原点,
![]() 所求的直线方程为
所求的直线方程为![]() .
.
20.解: ![]() 。设
。设![]() 的斜率为
的斜率为![]() ,则
,则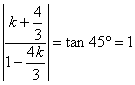 ,
,![]()
故所求的直线方程为:![]()
21.解:设甲煤矿调往东站的煤为![]() 万吨,乙煤矿调往东站的煤为
万吨,乙煤矿调往东站的煤为![]() 万吨,则
万吨,则
那么总运费:![]() 万元,
万元,
即![]() ,而
,而![]() 满足
满足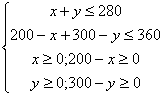 ,作出可行域,
,作出可行域,
 (略)设直线
(略)设直线![]() 与
与![]() 轴交点为
轴交点为![]() ,则.把直线
,则.把直线![]() 向上平移至M时
向上平移至M时![]() 最小。所以甲煤矿生产的煤全部运往西站;乙煤矿向东站运280万吨,向西站云20万吨时,总运费最少。
最小。所以甲煤矿生产的煤全部运往西站;乙煤矿向东站运280万吨,向西站云20万吨时,总运费最少。
22. 解:(1)![]()
![]() 设D的坐标为
设D的坐标为![]() 由于
由于
![]() 故
故![]() 又CD//OB
又CD//OB
![]() C的坐标为
C的坐标为![]()
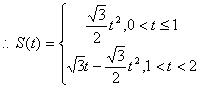 ,
,
(2)当![]() 时,
时,![]() .
.