高二上学期联合期中考试数学试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共100分。考试时间100分钟。
第I卷(选择题共40分)
一、选择题(本题共10小题,每题4分,共40分)
1.下列命题中,正确命题的个数是( A)
(1)各个侧面都是矩形的棱柱是长方体
(2)三棱锥的表面中最多有三个直角三角形
(3)简单多面体就是凸多面体
(4)过球面上二个不同的点只能作一个大圆
A.0个 B.1个 C.2个 D. 3个
2.在斜棱柱的侧面中,矩形最多有 ( A )个
A.2
B.
3. 已知直线a、b和平面M,则![]() 的一个必要不充分条件是( D )
的一个必要不充分条件是( D )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]() 与平面M成等角
与平面M成等角
4. 正四棱锥的一个对角面与一个侧面的面积之比为![]() ,则侧面与底面的夹角为( D )
,则侧面与底面的夹角为( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知α,β是平面,m,n是直线.下列命题中不正确的是.......................... ( A )
A.若m∥n,m⊥α,则n⊥α B.若m∥α,α∩β=n,则m∥n
C.若m⊥α,m⊥β,则α∥β D.若m⊥α,![]() ,则α⊥β
,则α⊥β
6.在的展开式中,只有第5项的二项式系数最大,则展开式中的常数项是( B )
(A)-7 (B)7 (C)-28 (D)28
7.已知棱长为2的正方体内有一个和各个面都相切的球体,则球体的表面积是 ( C )
(A)8![]() (B)6
(B)6![]() (C)4
(C)4![]() (D)2
(D)2![]()
8.如果三位数的十位数字既大于百位数字也大于个位数字,则这样的三位数一共有( A )
(A)240个 (B)285个 (C)231个 (D)243个(16)
9.一个骰子连续掷两次,以先后得到的点数m,n为点P (m,n),那么点P在圆x2 + y2 = 17外部的概率为 ( D )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.有一个正四棱锥,它的底面边长与侧棱长均为a,现用一张正方形包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小边长应为( B )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
第Ⅱ卷(非选择题共60分)
二、填空题(本题共6小题,每题5分,共30分)
11.![]() 的展开式中
的展开式中![]() 的系数是 -10 ,如果展开式中第
的系数是 -10 ,如果展开式中第![]() 项和第
项和第![]() 项的二项式系数相等,则
项的二项式系数相等,则![]() 等于 2 .
等于 2 .
12.边长为2的正方形ABCD在平面α内的射影是EFCD,如果AB与平面α的距离为![]() ,则AC与平面α所成角的大小是
30º
,则AC与平面α所成角的大小是
30º
13.现有甲种电脑56台,乙种电脑42台,如果用分层抽样的方法从中抽取一个容量为14的样本,则乙种电脑应抽样___6_____台.
14.三角形ABC的斜边AB在平面a内,直角边AC,BC与平面a所成的角分别为 30°、60°,则平面ABC与平面a所成的二面角的正弦值为______ 1________.
15.将棱长为1的正方体木块加工成一个体积最大的球,则这个球的体积为____![]() ___,球的表面积为__
___,球的表面积为__![]() ________(不计损耗)。
________(不计损耗)。
16.已知点P,直线![]() ,给出下列命题:
,给出下列命题:
①若![]() ②若
②若![]()
③若![]() ④若
④若![]()
⑤若![]()
其中正确命题的序号是_____②⑤________(把所有正确命题的序号都填上)。
三、解答题(本题共3小题,每小题10分,共30分)
17.在学校的科技活动日中,有六件科技作品在展台上排成一排展出.
(Ⅰ)求作品甲不在两端的概率;
(Ⅱ)求作品甲、乙相邻的概率.
解(Ⅰ)作品甲不在两端的概率![]() ……………………5分
……………………5分
=![]() ;……………………6分
;……………………6分
(Ⅱ)作品甲、乙相邻的概率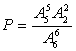 ……………………11分
……………………11分
作品甲、乙相邻的概率为![]() …………………………12分
…………………………12分
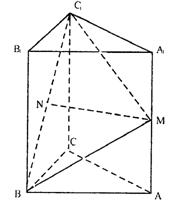
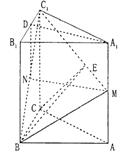
18.
|
(Ⅰ)求证:MN∥平面A1B
(Ⅱ)求二面角B-C
解:方法一(Ⅰ)取B
所以DN//BB1///AA1,………………1分
|
所以MN//A1D;…………3分
又![]() ,
,
所以MN//平面A1B
(Ⅱ)三棱柱ABC-A1B
又∠ACB=90°,所以BC⊥平面ACC
在平面ACC
则CE为BE在平面ACC
所以∠BEC为二面角B—C
由于△CEC1与三角形C![]()
所以![]() ……………………11分
……………………11分
所以![]() ……………………13分
……………………13分
|
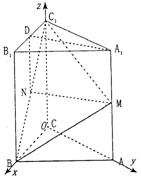
方法二(Ⅰ)如图,以点C为坐标原点,以CB所在
直线为Ox轴,CA所在直线为Oy轴,CC1所在直线
为Oz轴,建立空间直角坐标系.
由已知得![]() 、
、![]() 、
、![]() .
.
![]() ,
,![]() ,
,![]()
所以![]()
所以![]() …………2分
所以MN//A1N;………………4分
…………2分
所以MN//A1N;………………4分
又![]() 所以MN//平面A1B
所以MN//平面A1B
(Ⅱ)三棱柱ABC—A1B
![]() ………………7分
………………7分
设垂直于平面BMC1的向量![]()
所以![]() 即
即
所以![]() ……………………………………10分
……………………………………10分
所求二面角的大小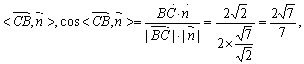 ……………13分
……………13分
即二面角B—C![]() …………………………14分
…………………………14分
19.直三棱柱ABC-A1B![]() ,E是A
,E是A![]() 且交AC于D,
且交AC于D,![]() 。
。
(I)证明:![]() 平面
平面![]() ;
;
(II)证明:![]() 平面
平面![]() ;
;
(III)求平面![]() 与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。
与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。
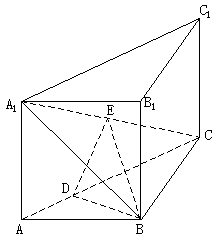
(I)证:
![]() 三棱柱
三棱柱![]() 中
中![]() , 1分
, 1分
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 3分
3分
(II)证:
![]() 三棱柱
三棱柱![]() 中
中![]() ,
,
![]() 中
中![]()
![]() 是等腰三角形 6分
是等腰三角形 6分
![]() E是等腰
E是等腰![]() 底边
底边![]() 的中点,
的中点,
![]()
又依条件知![]()
且![]()
由①,②,③得![]() 平面EDB 8分
平面EDB 8分
(III)解:
![]() 平面
平面![]() ,
,
且![]() 不平行,
不平行,
故延长![]() ,ED后必相交,
,ED后必相交,
设交点为E,连接EF,如下图
![]() 是所求的二面角 10分
是所求的二面角 10分
依条件易证明![]()
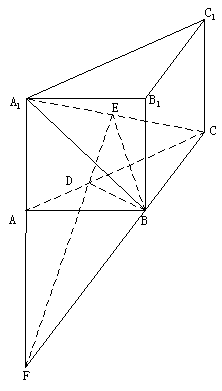
![]() 为
为![]() 中点,
中点,
![]() A为
A为![]() 中点
中点
![]()
![]()
![]()
即![]() 12分
12分
又![]() 平面EFB,
平面EFB,
![]()
![]() 是所求的二面角的平面角 13分
是所求的二面角的平面角 13分
![]() E为等腰直角三角形
E为等腰直角三角形![]() 底边中点,
底边中点,
![]()
故所求的二面角的大小为![]() 14分
14分