高中学生学科素质训练
高二上学期数学期末测试题
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一、选择题(本大题共12小题,每小题5分,共60分)
1.设集合![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.若不等式![]() 的解集为(-1,2),则实数a等于 ( )
的解集为(-1,2),则实数a等于 ( )
A.8 B.
3.若点(a,b)是直线x +2y+1=0上的一个动点,则ab的最大值是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.求过直线2x-y-10=0和直线x+y+1=0的交点且平行于3x-2y+4=0的直线方程
( )
A. 2x+3y+6=0 B. 3x-2y-17=0
C. 2x-3y-18=0 D. 3x-2y-1=0
5.圆![]() 的圆心到直线
的圆心到直线![]() 的距离是 ( )
的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如果双曲线的实半轴长为2,焦距为6,那么该双曲线的离心率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.7
D.7
7.过椭圆![]() 的焦点且垂直于x轴的直线l被此椭圆截得的弦长为 ( )
的焦点且垂直于x轴的直线l被此椭圆截得的弦长为 ( )
A.![]() B.
B.![]() C.3 D.
C.3 D. ![]()
8.椭圆![]() 为参数)的焦点坐标为 ( )
为参数)的焦点坐标为 ( )
A.(0,0),(0,-8) B.(0,0),(-8,0)
C.(0,0),(0,8) D.(0,0),(8,0)
9.点![]() 到曲线
到曲线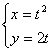 (其中参数
(其中参数![]() )上的点的最短距离为 ( )
)上的点的最短距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.抛物线的顶点在原点,对称轴为坐标轴,焦点在直线![]() 上,则抛物线的方程为 ( )
上,则抛物线的方程为 ( )
A.![]() B.
B. ![]()
C.![]() D.以上均不对
D.以上均不对
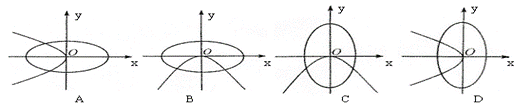
11.在同一坐标系中,方程![]() 的曲线大致是
的曲线大致是
( )
12.在直角坐标系xOy中,已知△AOB三边所在直线的方程分别为![]() ,
,
则△AOB内部和边上整点(即横、纵坐标均为整数的点)的总数是 ( )
A.95 B.
二、填空题(本大题共4小题,每小题4分,共16分)
13.椭圆![]() 的一个焦点是
的一个焦点是![]() ,那么
,那么![]() .
.
14.已知直线x =a (a>0) 和圆(x -1)2+ y 2 = 4 相切,那么a的值是
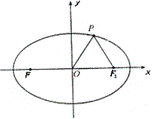
15.如图,F1,F2分别为椭圆![]() 的左、右焦点,点P在椭圆上,△POF2是面积为
的左、右焦点,点P在椭圆上,△POF2是面积为![]() 的正三角形,则b2的值是
.
的正三角形,则b2的值是
.
 16.函数
16.函数![]() 的定义域是
__.
的定义域是
__.
三、解答题(本大题共6小题,共74分)
17.解关于x的不等式:![]() .(12分)
.(12分)
18. 设![]() 为两定点,动点P到A点的距离与到B点的距离的比为定值
为两定点,动点P到A点的距离与到B点的距离的比为定值![]() ,求P点的轨迹. (12分)
,求P点的轨迹. (12分)
19.某厂用甲、乙两种原料生产A、B两种产品,已知生产1t A产品,1t B产品分别需要的甲、乙原料数,可获得的利润数及该厂现有原料数如下表所示.问:在现有原料下,A、B产品应各生产多少才能使利润总额最大?列产品和原料关系表如下:
|
| A产品 (1t) | B产品 (1t) | 总原料 (t) | ||
| 甲原料(t) | 2 | 5 | 10 | ||
| 乙原料(t) | 5 | 3 | 18 | ||
| 利润(万元) | 4 | 3 |
(12分)
20.已知抛物线的顶点在原点,它的准线经过曲线![]() 的右焦点,且与x轴垂直,
的右焦点,且与x轴垂直,
抛物线与此双曲线交于点(![]() ),求抛物线与双曲线的方程.(12分)
),求抛物线与双曲线的方程.(12分)
21. 已知点![]() 到两个定点
到两个定点![]() 、
、![]() 距离的比为
距离的比为![]() ,点
,点![]() 到直线
到直线![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程.(12分)
的方程.(12分)
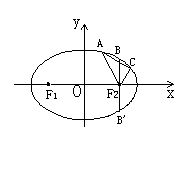 22.已知某椭圆的焦点是
22.已知某椭圆的焦点是![]() 、
、![]() ,过点F2并垂直于x轴的直线与椭圆的一个交点为B,且
,过点F2并垂直于x轴的直线与椭圆的一个交点为B,且![]() ,椭圆上不同的两点
,椭圆上不同的两点![]() 、
、![]() 满足条件:
满足条件:![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
(I)求该椭圆的方程;
(II)求弦AC中点的横坐标.(14分)
参考答案
一.选择题(本大题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | C | B | A | C | C | D | B | C | D | B |
二.填空题(本大题共4小题,每小题4分,共16分)
13.1 14.3
15.![]() 16.(-1,0)
16.(-1,0)
三.解答题(本大题共6小题,共74分)
17. (12分)
[解析]:原不等式可化为![]()
当a>1时有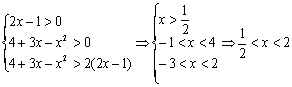
(中间一个不等式可省)
当0<a<1时有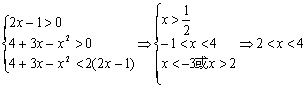
∴当a>1时不等式的解集为![]() ;
;
当0<a<1时不等式的解集为![]()
18.(12分)
[解析]:设动点P的坐标为(x,y). 由![]() .
.
化简得![]()
当![]() ,整理得
,整理得![]() .
.
当a=1时,化简得x=0.
所以当![]() 时,P点的轨迹是以
时,P点的轨迹是以![]() 为圆心,
为圆心,![]() 为半径的圆;
为半径的圆;
当a=1时,P点的轨迹为y轴.
19.(12分)
[解析]:设生产A、B两种产品分别为xt,yt,其利润总额为z万元,
 根据题意,可得约束条件为
根据题意,可得约束条件为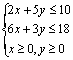
 作出可行域如图:
作出可行域如图:
目标函数z=4x+3y,
作直线l0:4x+3y=0,再作一组平行于l0的直线l: 4x+3y =z,当直线l经过P点时z=4x+3y取得最大值,
由![]() ,解得交点P
,解得交点P![]()
所以有![]()
所以生产A产品2.5t,B产品1t时,总利润最大,为13万元.
20.(12分)
[解析]:由题意可知抛物线的焦点到准线间的距离为
设抛物线的方程为![]() ∵抛物线过点
∵抛物线过点![]() ①
①
又知![]() ② 由①②可得
② 由①②可得![]()
∴所求抛物线的方程为![]() ,双曲线的方程为
,双曲线的方程为![]()
21.(12分)
[解析]:设点![]() 的坐标为
的坐标为![]() ,由题设有
,由题设有![]()
即![]()
整理得![]() ………①
………①
因为点![]() 到
到![]() 的距离为1,
的距离为1,![]()
所以∠![]()
![]()
![]() ,直线
,直线![]() 的斜率为
的斜率为![]()
直线![]() 的方程为
的方程为![]() ………②
………②
将②式代入①式整理得![]()
解得![]() ,
,![]()
代入②式得点![]() 的坐标为
的坐标为
![]() 或
或![]() ;
;![]() 或
或![]()
直线![]() 的方程为
的方程为![]() 或
或![]()
22.(14分)
[解析]:(I)由椭圆定义及条件知![]()
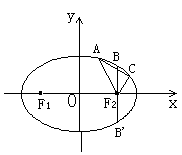 得
得![]() ,又
,又![]() , 所以
, 所以![]()
故椭圆方程为![]()
(II)由点B![]() 在椭圆上,得
在椭圆上,得
![]()
解法一:
因为椭圆右准线方程为![]() ,离心率为
,离心率为![]() .
.
根据椭圆定义,有![]() ,
, ![]()
由![]() ,
,![]() ,
,![]() 成等差数列,得
成等差数列,得![]() ,
,
由此得出![]() .设弦AC的中点为P
.设弦AC的中点为P![]() ,
,
则![]() .
.
解法二:
由![]() ,
,![]() ,
,![]() 成等差数列,得
成等差数列,得
![]() ,
,
由A![]() 在椭圆
在椭圆![]() 上,得
上,得![]()
所以![]()
![]()
同理可得![]()
将代入式,得![]() .
.
所以![]() 设弦AC的中点为P
设弦AC的中点为P![]()
则![]() .
.
