第二学期高二年级期中考试数学试卷 （文科实验班）
一、选择题：
1．设全集
=R，集合M=
，N=
，则下列关系中正确的是（ ）
A、M
B、M
C、M
D、（CuM）
2．已知
：x>1，q：
，则是q的（ ）
A、充分不必要条件 B、必要不充分条件
C、充分条件 D、既非充分又非必要条件
3．设函数f(x)是定义在R上的以3为周期的奇函数，若f(1)>1，f(2)=
，则
的取值范围是（ ）
A、
B、
C、
D、 
4．、等差数列
的公差d<0，且
=12，
，则数列的通项公式是（ ）
A、
B、
C、
D、
5．．已知P是函数
的图象上的点,若P点的横坐标为2， 且函数的图象在点P处的切线方程是
，则
的值是----------------------------( )
A. 
B. 
D. 不能确定
6．函数
的图象与
的图象关于
轴对称，若 
是的反函数，则函数
的单调递增区间是
(A) 
(B) 
(C)
(D) 
7．已知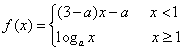
是(－∞，＋∞)上的增函数，那么实数a的取值范围是
(1，＋∞) (－∞，3) [，3) (1，3)
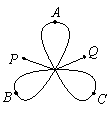
8．一个旅游景区如右图所示，某人从点P处进，点Q处出，游览三个景点A、B、C及沿途风光，则不同的游览线路种数最少为
6 8
12 48
9．将函数
的图象按向量a平移后，得到
的图象，则 （ ）
A．a=（1，2） B．a=（1，－2） C．a=（－1，2） D．a=（－1，－2）
10． 设
的展开式中x的一次项的系数，则
的值是（ ）
A．16 B．
二、填空题：
11．在等比数列{n}中，1=1, 
12．已知f(x)=kx+
(k
R)，f(-2)=0，则f(2)=_____________。
13． 已知函数f(x)=(
)x的图象与函数g(x)的图象关于直线y=x对称，令h(x)=g(1-
)，则关于h(x)有下列命题：
①h(x)的图象关于原点对称；②h(x)的最小值是1；③h(x)为偶函数；④h(x)在（0，1）上为减函数，其中正确的命题的序号是________。（将你认为正确的命题的序号都填上）
１4．已知
，则
__________________.
15．若关于
的不等式
恒成立，则实数的取值范围是
．
16. 数列
的前
项和记为
则
17. 5封不同的信,放入3个不同的信箱,且每封信投入每个信箱的机会均等,则3个信箱中放有信件数目的最大值为2时不同的投信的方法种数有
第二学期高二年级期中考试
数学答题卷(文科实验班)
一、选择题（每小题5分，请把正确的选项代号填入下表）
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
题号二、填空题（每小题4分，请把你的最简答案填在下面相应的横线上）
11、_________ 12、__________ 13、_________ 14、__________
15、_________ 16、__________ 17、_________
三.解答题:
18．甲、乙两支足球队经过加时赛比分仍为0：0，现决定各派5名队员，每人射一个点球决定胜负，假设两支球队派出的队员每人的点球命中概率均为0.5（相互独立）.
（1）如果不考虑乙球队，那么甲球队5名队员中有连续三名队员射中，而另两名队员未射中的概率是多少？
（2）甲、乙两队各射完5个点球后，再次出现平局的概率是多少？
19、已知函数f(x)=x3-3x
（1）求函数f(x)在[-3，
]上的最大值和最小值；
（2）过点P（2，-6）作曲线y=f(x)的切线，求此切线的方程。
20.已知数列{
}的前项和为Sn，且S4=4，当n≥2时，满足
（1）求证：{
}为等差数列；
（2）求数列{}的通项公式。
21.已知f(x)=xx-a+2x-3.
(I).当a=4,
时，问x分别取何值时，函数f(x)取得最大值和最小值，并求出相应的最大值和最小值；
（II）.求a 的取值范围，使得f(x)在R上恒为增函数;
（III）.已知常数a=4,数列{an} 满足an+1= (n∈N*),试探求
的值，使得数列{an}(n∈N*)成等差数列。
22.已知
，
的反函数为
，点
在曲线
上
，且
(I)求的表达式；
(II)证明数列{
}为等差数列；
(Ⅲ)设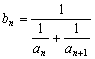
,记
，求