第二学期期中考试高二数学试卷2
本试卷满分150分 考试时间120分钟 命题人：彭玉宏
一、选择题：本大题共12小题，每小题5分，共60分．
1、已知五条直线中的任意三条共面，那么这五条直线 （ ）
A、必共面 B、不一定共面 C、交于一点 D、互相平行
2、下列说法正确的是 （ ）
A、直线a平行于平面M，则a平行于M内的任意一条直线
B、直线a与平面M相交，则a不平行于M内的任意一条直线
C、直线a不垂直于平面M，则a不垂直于M内的任意一条直线
D、直线a不垂直于平面M，则过a的平面不垂直于M
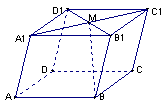
3、如图：在平行六面体
中，
为
与
的交点。若
，
，
，则下列向量中与
相等的向量是（ ）
A、 
B、 
C、
D、
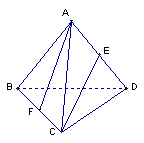
4、如图：在棱长都相等的四面体
中，
、
分别
为棱
、
的中点，连接
、
，则直线、所
成角的余弦值为 （ ）
A、
B、
C、
D、
5、一个正多面体的面数F与顶点数V满足关系式2V=
A、三角形 B、四边形 C、五边形 D、六边形
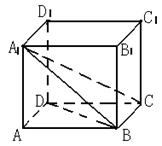6、如图，在直平行六面体
中，异面直线 
和BD所成的角为
，
和 
所成的角不等于，则四边形ABCD （ ）
A、不是矩形，不是菱形； B、不是矩形，是菱形；
C、是矩形，不是菱形； D、是正方形。
7、点（x，y，z）关于y轴的对称点的坐标是 （ ）
A、
B、
C、
D、
8、底面边长为a，侧棱长为b的正四棱柱的外接球的表面积为 （ ）
A、
B、
C、
D、
9、已知空间四点 A（2，1，
），B（ 
），C（3，0，1），D（1，4，m），若A、B、C、D四点共面，则m=（ ）
A、
B、
C、19
D、5
10、正方体ABCD—A1B
A．线段B
C．BB1中点与CC1中点连成的线段 D．BC中点与B
11、若地球半径为R，在北纬45°圈上有A、B两点，且这两点间的球面距离为
，则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 （ ）
A、
B、
C、
D、
12、已知AB是异面直线a、b的公垂线段，AB=2，且a与b成
角，在直线a上取AP=4，则点P到直线b的距离为
（ ）
A、
B、
D、或
第二学期期中考试高二数学答卷2
一、选择题：本大题共12小题，每小题5分，共60分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
13、边长为2的正方形ABCD的边CD在平面
内，AB在平面外，如果AB与平面的距离为
，则对角线AC与平面所成角的大小是_____________。
14、已知S是△ABC所在平面外一点， D是SC的中点，若
＝
， 则
x＋y＋z＝ 。
15、球的半径为8，经过球面上一点作一个平面，使它与经过这点的半径成
角，则这个平面截球的截面面积为______________。
16、正四面体ABCD中，点A（0，0，0），B（2，0，0），C（1，
，0），则点D的坐标为___________________________。
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．
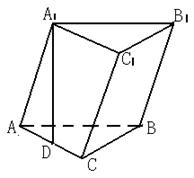17、（12分）斜三棱柱
中，
，AC=BC=a，点
在底面ABC上的射影D恰为AC的中点，又知
。（1）求证：BC⊥平面 
；（2）求点到AB的距离；（3）求二面角
的余弦值。
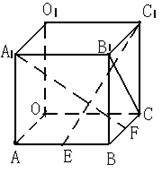
18、（12分）如图，正方体的一个顶点为O，OA、OB、OC是有一个公共点O的三个面上的对角线，OQ为体对角线。（1）求
与
的关系；（2）沿
、
、
方向分别作用
19、（12分）在棱长为
的正方体
中，E，F分别为棱AB，BC上的动点，且AE=BF，（1）求证：
；（2）若F为棱BC的中点，求异面直线
与
的距离。
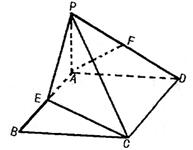20、（12分）如图，PA⊥平面ABCD，四边形ABCD是矩形，点E在边AB上，F为PD的中点，AF∥平面PCE，（1）试确定E点位置； （2）若二面角
为，AD=2，CD=3，求直线AF到平面PCE的距离。
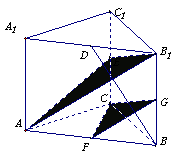21、（14分）如图，在直三棱柱ABC—A1B
（1）证明：BD⊥平面AB1E；
（2）证明：平面AB1E//平面CFG；
（3）求直线AC与平面AB1E所成的角。
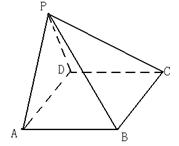22、（12分）如图，四棱锥
的底面ABCD为矩形，
PA⊥AB， AD=5， PA=4，cos∠PAD=
。
（1）求证：平面PDC⊥平面PAB；（2）如果AB=3，在棱AB上是否存在一点Q，使异面直线CQ与DP所成的角为
？如果存在，求出AQ∶QB的值；如果不存在，请说明理由。