第一学期期末模拟试题数学卷

第一学期期末模拟试题数学卷

（时间120分钟，满分160分）

一、选择题（每题5分，共50分）

1．任何一个算法都必须有的基本结构是（　 ）．

　　　 A 顺序结构　　　　　　　B 条件结构　　　　　　　C 循环结构　　　　　　　D 三个都有

2．线性回归方程表示的直线必经过的一个定点是 (  )

(A) 　　　 (B) 　　　　(C) 　　　　(D)

3．若样本的方差是2，则样本的标准差为（ C　 ）

A．2　　　　　 B．4  　　　　　C．　　　　　 D．8

n←5 　　 s←0 　 While s<14 s←s+n n←n-1 End while Print　n （第5题）

4．某班委会由4名男生与3名女生组成，现从中选出2人担任正副班长，至少有1名女生当选的概率为　　　　　　　　　　　　  　　　　　　　　　　　　　（ C　 ）

A．　　　　　 B．　　　　　  C．　　　　　 D．

5．下列程序执行后输出的结果是(　　 )

A、-1　　  B、0　　　　C、1　　　　D、2

6．双曲线的渐近线方程为，则双曲线的离心率为　 （ D　 ）

A．　　　　　 B．　　　　  C．或　　　　D．

7． 国家机关用监听录音机记录了两个间谍的谈话，发现了30 min长的磁带上，从开始30s处起，有10s长的一段内容包含两间谍犯罪的信息，后来发现，这段谈话的一部分被某工作人员擦掉了，该工作人员声称她完全是无意中按错了键，使从此处起往后的所有内容都被擦掉了，那么由于按错了键使含有犯罪内容的谈话被部分或全部擦掉的概率为（　 ）

A．　　　　　 B．　　　　　  C．　　　　　 D．

8．已知两定点F₁(-1,0) 、F₂(1,0), 且是与的等差中项,则动点P的轨迹是（　 ）

　  A. 椭圆 　　　 B. 双曲线　　　　C. 抛物线　　　　  D. 线段

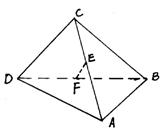
9．（理科做）如图所示，在四面体ABCD中，E、F分别是AC与BD的中点，若CD = 2AB = 4，EF⊥BA，则EF与CD所成角为（　 ）　

　　　 A．90⁰　　　B．45⁰　C．60⁰　 D．30

（文科做）函数内是减函数，则（　 ）

A、　 B、　 C、　 D、

10．已知命题P：若，则，命题Q：若，则。若P为真且Q的否命题为真，则“”是“的”　　　　　　　　　　　　　　　　　  （　A  ）

A．充分条件　　　 B．必要条件　　　 C．充要条件　　　D．既不充分也不必要条件

二、填空题（每题6分，共36分）

11．命题“”的否定是　　　　　　　　　　　　　　　　　　　　 ．

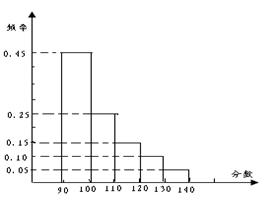
12．某市高三数学抽样考试中，对90分以上（含90分）的成绩进行统计，其频率分布图如图所示，若130-140分数段的人数为90人，则90-100分数段的人数为　　　　　　

13．（理科做） 已知A（1，1，1），B（－1，0 ，4），C（2 ，－2，3），则〈，〉的大小为__________

（文科做）函数的最大值为__________

14．已知抛物线，焦点为F，过F作直线L交抛物线于A、B两点，则__________

15．根据如图所示的伪代码，可知输出结果为__________

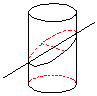16如图所示, 底面直径为的圆柱被与底面成的平面所截，其截口是一个椭圆，则这个椭圆的离心率为　　 　　　　　 ．

			I←1 While I<8  S←2I+3 I←I+2 End　while Print S （第15题图）
	第12题图

三、解答题：（解答应写出文字说明，证明过程和演算步骤写在答卷上）

17．已知椭圆的两焦点为，P为椭圆上一点，且

（1）求椭圆的方程。 　（2）若点P在第二象限，，求的面积。

18．一次口试，每位考生要在8道口试题中随机抽出2道题回答，若答对其中1题即为及格。（1）现有某位考生会答8道题中的5道题，那么，这位考生及格的概率有多大？

（2）如果一位考生及格的概率小于50％，则他最多只会几道题？

19一顶点在坐标原点，焦点在x轴上的抛物线截直线所得的弦长为，求抛物线的方程。并写出焦点坐标，准线方程。

 

第一学期末模拟试题高二数学答题卷

一、选择题（每小题5分，共50分）

题 号	1	2	3	4	5	6	7	8	9	10
答 案

二、填空题（每小题6分，共36分）

11．________________.　　　 12. ________________.　13. ________________.

14．________________.　　　 15________________　　16.________________.

三、解答题：（本大题共5小题，12+14+16+16+16=74′）

17．

18．

19．

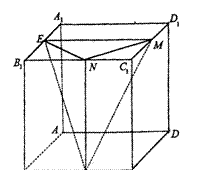
20．（理科做）如图，正方体ABCD—A₁B₁C₁D₁的棱长为1，E、F、M、N分别是A₁B₁、BC、C₁D₁、B₁C₁的中点.（I）用向量方法求直线EF与MN的夹角；

（II）求直线MF与平面ENF所成角的余弦值；

（III）求二面角N—EF—M的平面角的正切值.

（文科做）已知长、宽分别为16，10的矩形纸板，在其四个角处分别截去相同的小正方形做出一个无盖的盒子，求盒子的最大容积。

21．设F₁, F₂分别为椭圆C: (a>b>0)的左、右两个焦点，

（1）若椭圆C上的点A(1, )到F₁, F₂两点的距离之和等于4，写出椭圆C的方程；

（2）设K是（1）中所得椭圆上的动点，求线段F₁K的中点的轨迹方程；

（3）过作椭圆的弦AB，若△的周长为16，椭圆的离心率为，求椭圆的标准方程。