第一学期期中考试高二数学试卷2

2007学年第一学期期中考试高二数学试卷2

一、选择题（每小题只有一个正确答案。每小题5分，共60分。）

1． 已知点A (1, 2)、B (1, 3)，则直线AB倾斜角为　　　　　　　　　　　　　　　　　　　　　　　（　 ）

　  A．0　　　　　　　　　　 B．　　　　　　　　　　C．arctan　　　　　 D．arctan

2． 直线y = 2与直线x + y – 2 = 0的夹角是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （ 　）

　  A．　　　　　　　　　 B．　　　　　　　　　　C．　　　　　　　　　　D．

3． 已知圆C的半径为2，圆心在x轴的正半轴上，直线3x + 4y + 4 = 0与圆相切，则圆C方程　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　  A．x² + y² – 2x – 3 = 0　　　　　　　　　　　　　　B．x² + y² + 4x = 0

　　C．x² + y² + 2x – 3 = 0　　　　　　　　　　　　　 D．x² + y² – 4x = 0

4． 圆x² + y² – 4x = 0在点P (1,)处的切线方程为　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　  A．x +y – 2 = 0　　　　　　　　　　　　　　　　 B．x +y – 4 = 0

　  C．x –y + 4 = 0　　　　　　　　　　　　　　　　 D．x –y + 2 = 0

5． 不等式x +> 2的解集是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　 ）

　  A．(– 1, 0) È (1, + ¥)　　　　　　　　　　　　　　 B．(– ¥, – 1) È (0, 1)

　  C．(– 1, 0) È (0, 1)　　　　　　　　　　　　　　　　 D．(– ¥, – 1) È (1, + ¥)

6． 已知a、b、c满足c < b < a，且ac < 0，那么下列选项中不一定成立的是（ 　）

　  A．ab > ac　　　　　　　　　B．c (b – a) > 0 　　C．cb² > ab²　　　　　D．ac (a – c) < 0

7． 若，则下列不等式① a + b < ab；② a > b ；③ a < b；④中，正确的不等式有　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　  A．1个　　　　　　　　B．2个　　　　　　　　　C．3个　　　　　　　　 D．4个

8． 如果直线x + ay + 6 = 0与直线(a – 2)x + 3y + 2a = 0平行，那么系数a为 （　 ）

　  A．3　　　　　　　　　　 B．– 1 　　　　　　　　　 C．3或– 1　　　　　　　　　 D．

9． 曲线与曲线 (16 < m < 25)的　　　　　　　　　　　　（　 ）

　  A．长、短轴相等　　　　　　　　　　　　　　　　　B．焦距相等

　  C．离心率相等　　　　　　　　　　　　　　　　　　　D．准线相等

10．如果双曲线上一点P到右焦点的距离为，那么点P到左准线的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　 ）

　  A．　　　　　　　　　B．13 　　　　　　　　　　C．5　　　　　　　　　　　D．

11．已知直线y = kx + 1与双曲线x² – 2y² = 1有且仅有一个公共点，则实数k的值有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　 ）

　  A．1个　　　　　　　　B．2个　　　　　　　　　C．3上　　　　　　　　 D．4个

12．曲线y² = 4x关于直线x = 2对称的曲线方程是　　　　　　　　　　　　　　　　　　　　　　　（　 ）

　  A．y² = 8 – 4x　　　B．y² = 4x – 8 　　　C．y² = 16 – 4x　　 D．y² = 4x – 16

二、填空题（每小题4分，共16分）

13． 抛物线y =x²的焦点坐标是____________。

14．过点P (2, 3)，并且在两坐标轴上的截距相等的直线方程为____________。

15．设x，y满足约束条件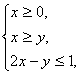： 则z = 3x + 2y的最大值是____________。

16．已知 则不等式x + (x + 2)·f (x + 2) £ 5的解集是__________。

第一学期期中考试

高二数学试卷

一、选择题（每小题只有一个正确答案。每小题5分，共60分。）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题（每小题4分，共16分）

13．____________　14．____________　15．____________　16．____________

三、解答题（共6小题，共74分。）

17．(1) 设0 < x < 2，求函数f (x) =的最大值；

　　(2) 解不等式1 < 1 – x² < 3。

18．其家具厂有方木料90m³，五合板600m²，准备加工成书桌和书橱出售。已知生产每张书桌需方木料0.1m³，五合板2m²，生产每个书橱要方木料0.2m²，五合板1m²。出售一张书桌可获利润80元，出售一张书橱可获利润120元，怎样安排生产可使即得利润最大？

19．在DABC中，BC边上的高所在直线的方程为x – 2y + 1 = 0，ÐA的平分线所在直线的方程为y = 0，若点B的坐标为(1, 2)，求点A和点C的坐标。

20．已知椭圆。

(1) 若它的一条弦AB被点M (1, 1)平分，求AB的直线方程；

(2) 求过点M (1, 1)的弦的中点轨迹方程。

21．已知圆满足①截y轴所得弦长为2，②被x轴分成两段圆孤，其弧长的比为3 : 1，③圆心到直线l: x – 2y = 0的距离为，求该圆的方程。

22．直线l: y = kx + 1与双曲线C: 2x² – y² = 1的右支交于不同的两点A、B。

　　(1) 求实数k的取值范围；

　　(2) 是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，求出k的值；若不存在，说明理由。