珠海市斗门区第一中学解析几何单元测试题数学(文 科)
一、选择题本题共有10个小题,每小题5分;在每小题给出的四个选项中,只有一项是符合题目要求的,把正确选项的代号填在试卷指定的位置上。
1.已知A(2,3),B(-1,4)则直线AB的斜率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 如果椭圆![]() 上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )A. 10 B.
上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )A. 10 B.
3.已知点![]() 的坐标满足
的坐标满足![]() ,则动点P的轨迹是( )
,则动点P的轨迹是( )
A.椭圆 B.双曲线 C.两条射线 D.以上都不对
4.直线3x-2y=4的截距式方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. 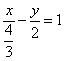
5.椭圆![]() 的焦点在
的焦点在![]() 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C. 2 D.4
C. 2 D.4
6. 若双曲线![]() 的渐近线l方程为
的渐近线l方程为![]() ,则双曲线焦点F到渐近线l的距离为 ( )
A.2 B.
,则双曲线焦点F到渐近线l的距离为 ( )
A.2 B.![]() C.
C.![]() D.2
D.2![]()
7.若直线![]() 过点
过点![]() ,且
,且![]() 与双曲线
与双曲线![]() 只有一个公共点,则这样的直线有( )
只有一个公共点,则这样的直线有( )
A. 1条 B. 2条 C. 3条 D. 4条
8.双曲线两条渐近线的夹角为60º,该双曲线的离心率为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或2 D.
或2 D.![]() 或2
或2
9.已知![]() , A、B分别在y轴和x轴上运动, O为原点,
, A、B分别在y轴和x轴上运动, O为原点, ![]() 则动点P的轨迹方程是
(
).
则动点P的轨迹方程是
(
).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.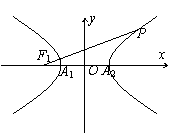 如图,双曲
如图,双曲![]() 的左焦点为F1,顶点为A1,
的左焦点为F1,顶点为A1,
A2,P是双曲线上任意一点,则分别以线段PF1、A
径的两圆位置关系为( )
A. 相切 B. 相交
C. 相离 D. 以上情况都有可能
二、填空题(本大题共4小题,每小题5分,共20分)
11.过点P(-2, -4)的抛物线的标准方程为
12. 若一双曲线的离心率为![]() ,则其渐近线为______________.
,则其渐近线为______________.
13.圆心在直线2x-y-7=0上的圆C与y轴交于两点A(0,-4)、B(0,-2),则圆的方程为_________.
14.已知平面上有两定点A,B,同一平面上一动点P与两定点的连线的斜率乘积等于常数m
(![]() ),对于下面5种曲线:① 直线;② 圆;③ 抛物线;④ 双曲线;⑤ 椭圆.则动点P的轨迹方程是____________________(将所有可能的情况都写出来)
),对于下面5种曲线:① 直线;② 圆;③ 抛物线;④ 双曲线;⑤ 椭圆.则动点P的轨迹方程是____________________(将所有可能的情况都写出来)
三、解答题(本大题6小题,共80分)
15.(本题满分12分)已知双曲线的中心在原点,焦点为F1![]() ,F2(0,
,F2(0,![]() ),
),
且离心率![]() ,求双曲线的标准方程.
,求双曲线的标准方程.
16.(本题满分13分) 已知圆C:![]() ,点P(2,-1),过P点作圆C的切线PA,PB,A,B为切点.
,点P(2,-1),过P点作圆C的切线PA,PB,A,B为切点.
(1)求切线长![]() .
.
(2)求直线AB的方程.
17.(本题满分13分)在椭圆![]() +
+![]() =1内有一点M(4, -1),使过点M的弦AB的中点正好为点M,求弦AB所在的直线的方程.
=1内有一点M(4, -1),使过点M的弦AB的中点正好为点M,求弦AB所在的直线的方程.
18. (本题满分14分)设动圆P过定点A(-3,0),并且在定圆B:![]() 的内部与其内切,求动圆的圆心P的轨迹方程.
的内部与其内切,求动圆的圆心P的轨迹方程.
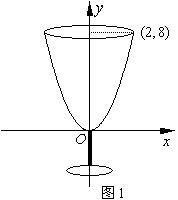
19.(本题满分14分)小明家中有两种酒杯,一种酒杯的轴截面是等腰直角三角形,称之为直角酒杯(如图1),另一种酒杯的轴截面近似一条抛物线,杯口宽
⑴ 请选择适当的坐标系,求出抛物线酒杯的方程.
⑵ 一次,小明在游戏中注意到一个现象,若将一些大小不等的玻璃球依次放入直角酒杯中,则任何玻璃球能触及酒杯杯底.但若将这些玻璃球放入抛物线酒杯中,则有些小玻璃球能触及酒杯杯底.小明想用所过数学知识研究一下,当玻璃球的半径r为多大值时,玻璃球一定会触及酒杯杯底部.你能帮助小明解决这个问题吗?

20.(本题满分14分)椭圆E的中心在原点O,焦点在x轴上,离心率e=![]() ,过点C(-1,0)的直线
,过点C(-1,0)的直线![]() 交椭圆于A,B两点,且满足
交椭圆于A,B两点,且满足![]()
(1)
若![]() 为常数,试用直线
为常数,试用直线![]() 的斜率k(k≠0)表示三角形OAB的面积.
的斜率k(k≠0)表示三角形OAB的面积.
(2)
若![]() 为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程.
为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程.
(3)
若![]() 变化,且
变化,且![]() =k2+1,试问:实数
=k2+1,试问:实数![]() 和直线
和直线![]() 的斜率k(k∈R),分别为何值时,椭圆E的短半轴长取得最大值?并求此时的椭圆方程.
的斜率k(k∈R),分别为何值时,椭圆E的短半轴长取得最大值?并求此时的椭圆方程.
斗门区一中解析几何单元测试题答题卷
考试时间:
一、选择题(每题5分共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | B | D | A | C | C | D | B | A |
二、填空题(每题5分共20分)
11.![]() 或
或![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() ①②④⑤
①②④⑤
三、解答题
15. 解:设双曲线的标准方程为![]() 则
则
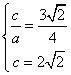 得
得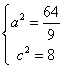
由![]() 知
知![]() ,即知双曲线的方程为
,即知双曲线的方程为![]()
 故所求的双曲线方程为
故所求的双曲线方程为![]() .
.
16. 解:由题意知圆C的圆心为 C(1,2),而P点坐标
为P(2,-1).
(1) 切线长![]()
![]()
![]()
(2) (法一)设过P的切线方程为![]() .
.
①当k不存在时,显然不成立
②当k存在时,![]() ,圆的半径为
,圆的半径为![]() ,
,
由点直线的距离公式知
![]() ,得
,得![]()
故所求的切线方程为x+y-1=0或7x-y-15=0
联立方程![]() 得
得![]() ,
,
由![]() 知
知![]() 得
得![]() 故
故
即知AB的方程为![]()
(法二)以P为圆心,以切线长为半径作圆得
![]() ,而AB是圆C与圆P的相交弦
,而AB是圆C与圆P的相交弦
故AB方程为![]()
17. 解:本题有四种方法,若用斜率,应该考虑斜率不存在,联立方程时二次项系数为0,及![]() 等问题.
等问题.
(法一) 由题意,M(4,-1)在圆内,则一定存在直线AB,使得M是AB的中点,设A(x,y),则B(8-x,-2-y),则
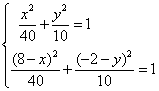 两式相减得
两式相减得![]() .
.
(法二) 题意,M(4,-1)在圆内,则一定存在直线AB,使得M是AB的中点.由公式![]() 知
知![]() ,知
,知![]()
故y+1=x-4,即得AB的方程为![]() .
.
18. 解:设动圆P的圆心P(x,y),半径为r.
由题意得圆B的半径R=8,PA=r,而在圆B内部与其内切,可知PB=8-r,即得PA+PB=8,由于AB=6,得P点的轨迹是椭圆,且
 a=4,c=3,
a=4,c=3,![]() ,即知动圆P的圆心P的轨迹为
,即知动圆P的圆心P的轨迹为![]()
19.解:⑴ 如图1,以杯底中心为原点,建立直角坐标系,
设抛物线方程为x2=2py( p>0).
将x=2,y=8代入抛物线方程,得p=![]() ,
,
∴ 抛物线方程为![]() .
.
⑵ (以下是我的理解)由题意,要想玻璃珠触及杯底,只需在y轴上找一点P(0,r),使得抛物线上的点到P点距离最近的点是顶点O即可.
设抛物线上任一点M(x,y),则![]() ,联立抛物线方程得
,联立抛物线方程得
![]() (y≥0)
(y≥0)
对称轴为y=![]() ,当对称轴
,当对称轴![]() 0时,可知
0时,可知![]() 在y≥0时是增函数,即当y=0时有最小值,也即最近点是原点O.
在y≥0时是增函数,即当y=0时有最小值,也即最近点是原点O.
故![]() ≤
≤![]() ,即当0<r≤
,即当0<r≤![]() 时,玻璃球一定会触及杯底
时,玻璃球一定会触及杯底
(以下是标准答案)设圆心在y轴正半轴上,且过原点的圆的方程为x2+( y-r)2=r2,将之代入抛物线方程,消去x,得y2+(![]() -2r)y=0. ∴ y1=0,y2=2r-
-2r)y=0. ∴ y1=0,y2=2r-![]() .
.
若要使玻璃球在杯中能触及杯底,则要y2=2r-![]() ≤0.
≤0.
即当0<r≤![]() 时,玻璃球一定会触及杯底.
时,玻璃球一定会触及杯底.
20. 解:设椭圆方程为:![]() ,由
,由![]() 及
及![]() ,
,
得![]() ,故椭圆方程为:
,故椭圆方程为:![]() ①
①
⑴直线![]() 交椭圆于A
交椭圆于A![]() ,B
,B![]() 两点,
两点,
由![]() 得
得![]()
即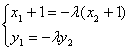 ②
②
把![]() 代入椭圆方程得:
代入椭圆方程得:
![]()
∴![]() ③
③ ![]() ④
④
∴![]()
由②③知道![]() ∴
∴![]()
⑵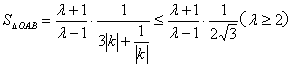
当且仅当![]() 时,即
时,即![]() 时,S取得最大值。
时,S取得最大值。
将![]() 代入③④中得
代入③④中得![]() ,故所求
,故所求![]()
⑶由②③联立得![]() 将
将![]() 代入④得
代入④得![]()
当![]() 时,
时,![]() 是
是![]() 的减函数,
的减函数,
故当![]() =2时
=2时![]() 故椭圆方程为
故椭圆方程为![]() 。
。