资阳市2005—2006学年度高中二年级第一学期期末质量检测
文 科 数 学
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 第Ⅰ卷1至2页,第Ⅱ卷3至8页. 全卷共150分,考试时间为120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.
3.考试结束时,将本试卷和答题卡一并收回.
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.抛物线![]() =-2y2的准线方程是( ).
=-2y2的准线方程是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2 . 已知过点A(-2,m)和B(m,4)的直线的斜率为-2,则m的值为( ).
A.10 B.2 C.0 D.-8
3.不等式![]() ≤0的解集是(
).
≤0的解集是(
).
A.{x│x≤2} B.{x│1<x≤2= C. {x│1≤x≤2} D.{x│1≤x<2=
4.圆![]() 的圆心到直线
的圆心到直线![]() 的距离是(
).
的距离是(
).
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
5.若a、b、c、d∈R,且![]() ,则下列命题正确的是(
).
,则下列命题正确的是(
).
A.a c>b
d
B.![]()
C.![]() D.
D.![]()
6.若直线l的斜率k满足1≤k≤![]() ,则直线l的倾斜角的取值范围是( ).
,则直线l的倾斜角的取值范围是( ).
A.![]() B.
B.![]()
C.![]()
![]() D.
D.![]()
7. 过点(1,2)且与直线 x+2y=0垂直的直线的方程为( ).
A.y=2x-3 B.y=2x
C.y=-![]() x+
x+![]() D.y=-
D.y=-![]() x+2
x+2
8.曲线y=![]() x3-x2+5在x=1处的切线的斜率是( ).
x3-x2+5在x=1处的切线的斜率是( ).
A.x2-2x B.0 C.1 D.-1
9.若A是定直线l外的一定点,则过A且与l相切圆的圆心轨迹是( ).
A.圆 B.椭圆 C.抛物线 D.双曲线一支
10
. 设![]() ,
,![]() ,则x、y之间的大小关系是( ).
,则x、y之间的大小关系是( ).
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
11. 若双曲线![]() 的焦点在y轴上,则m的取值范围是( ).
的焦点在y轴上,则m的取值范围是( ).
A.(-2,2) B.(1,2) C.(-2,-1) D.(-1,2)
12.已知椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一水平放置的椭圆形台球盘,其长轴长为2a,焦距为2c,若点A,B是它的焦点,当静放在点A的小球(不计大小),从点A沿直线出发,经椭圆壁反弹后再回到点A时,小球经过的路程是( ).
A.4a B.2(a-b) C.2(a+c) D.不能惟一确定
资阳市2005—2006学年度高中二年级第一学期期末质量检测
文 科 数 学
第Ⅱ卷(非选择题 共90分)
| 题号 | 二 | 三 | 总分 | 总分人 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷上.
2.答卷前将密封线内的项目填写清楚.
 |
二、填空题:本大题共4个小题,每小题4分,共16分.把答案直接填在题中横线上.
13. 用“<”或“>”填空:如果0<a<b<1,n∈N*,那么![]() ______
______![]() _______1 .
_______1 .
14. 若实数![]() 满足条件
满足条件![]() 则
则![]() 的最大值是__________.
的最大值是__________.
15. 过点(2,0)与圆![]() 相切的直线的条数是__________.
相切的直线的条数是__________.
16. 给出下列四个命题:① 两平行直线![]() 和
和![]() 间的距离是
间的距离是![]() ;② 方程
;② 方程![]() 不可能表示圆;③ 若双曲线
不可能表示圆;③ 若双曲线![]() 的离心率为e,且
的离心率为e,且![]() ,则k的取值范围是
,则k的取值范围是![]() ;④ 曲线
;④ 曲线![]() 关于原点对称.其中所有正确命题的序号是_____________ .
关于原点对称.其中所有正确命题的序号是_____________ .
三、解答题: 本大题共6个小题,共74分.解答应写出必要的文字说明,证明过程或演算步骤.
 17. (本小题满分12分)
17. (本小题满分12分)
(Ⅰ) 比较下列两组实数的大小:
① ![]() -1与2-
-1与2-![]() ; ② 2-
; ② 2-![]() 与
与![]() -
-![]() ;
;
(Ⅱ) 类比以上结论,你能否得出更一般的结论?证明你的结果.
 18. (本小题满分12分)
18. (本小题满分12分)
已知直线l过点M(0,1),且l被两已知直线l1:x-3y+10=0和l2:2x+y-8=0所截得的线段恰好被M所平分,求直线l方程.
 19. (本小题满分12分)
19. (本小题满分12分)
已知圆C同时满足两个条件:①圆心是直线![]() 与
与![]() 的交点;②直线
的交点;②直线![]() 与圆C相切. 求圆C的方程.
与圆C相切. 求圆C的方程.
 20. (本小题满分12分)
20. (本小题满分12分)
已知抛物线的顶点在原点,它的准线经过双曲线![]() 的左焦点,且与x轴垂直,抛物线与此双曲线交于点(
的左焦点,且与x轴垂直,抛物线与此双曲线交于点(![]() ),求抛物线与双曲线的方程.
),求抛物线与双曲线的方程.

21. (本小题满分12分)
解关于x的不等式![]() (
(![]() ).
).

22. (本小题满分14分)
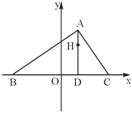
在△ABC中,已知B(-2,0)、C(2,0),AD⊥BC于点D,△ABC的垂心为H,且![]() .
.
(Ⅰ) 求点H(x,y)的轨迹G的方程;
(Ⅱ) 已知P(-1,0)、Q(1,0),M是曲线G上的一点,判断![]() ,
,![]() ,
,![]() 能否构成等差数列. 若能,求出M点的坐标;若不能,请说明理由.
能否构成等差数列. 若能,求出M点的坐标;若不能,请说明理由.
资阳市2005—2006学年度高中二年级第一学期期末质量检测
数学试题参考答案及评分意见
一、选择题:每小题5分,共60分.
1-5. DDBAC;6-10. BBDCA;11-12. CD.
二、填空题:每小题4分,共16分.
13. >,>; 14. 11; 15. 2; 16. ①,④.
三、解答题:每小题5分,共60分.
17.
(Ⅰ) ① (![]() +
+![]() )2-(2+1)2=2
)2-(2+1)2=2![]() -4>0.
-4>0.
故![]() +
+![]() >2+1,即
>2+1,即![]() -1>2-
-1>2-![]() .················································· 4分
.················································· 4分
② (2+![]() )2-(
)2-(![]() +
+![]() )2=4
)2=4![]() -2
-2![]() =2
=2![]() -2
-2![]() >0.
>0.
故2+![]() >
>![]() +
+ ![]() ,即2-
,即2-![]() >
>![]() -
-![]() . 7分
. 7分
(Ⅱ) 一般结论:若n是正整数,则![]() -
-![]() >
>![]() -
-![]() .······ 10分
.······ 10分
证明:与(Ⅰ)类似(从略).······································································· 12分
18.
过点M与x轴垂直的直线显然不合要求,故可设所求直线方程为y=kx+1,
············································································································· 2分
若此直线与两已知直线分别交于A、B两点,则解方程组可得
xA=![]() ,xB=
,xB=![]() .········································································ 6分
.········································································ 6分
由题意![]() +
+![]() =0,
=0,
∴k=-![]() . 10分
. 10分
故所求直线方程为x+4y-4=0.···························································· 12分
另解一:设所求直线方程y=kx+1,
代入方程(x-3y+10)(2x+y-8)=0,
得(2-5k-3k2)x2+(28k+7)x-49=0.
由xA+xB=-![]() =2xM=0,解得k=-
=2xM=0,解得k=-![]() .
.
∴直线方程为x+4y-4=0.
另解二:∵点B在直线2x-y-8=0上,故可设B(t,8-2t),由中点公式得A(-t,2t-6).
∵点A在直线x-3y+10=0上,
∴(-t)-3(2t-6)+10=0,得t=4.∴B(4,0).故直线方程为x+4y-4=0.
19.
解:由![]() 得交点
得交点![]() ,即所求圆的圆心为
,即所求圆的圆心为![]() .·························· 5分
.·························· 5分
设所求的方程为![]() ,·································································· 7分
,·································································· 7分
则![]() ,
,
故圆的方程为![]() .··········································································· 12分
.··········································································· 12分
20.
由题意可知抛物线的焦点到准线间的距离为2C(即双曲线的焦距).
设抛物线的方程为![]() 4分
4分
∵抛物线过点![]() ①
①
又知![]() ② 8分
② 8分
由①②可得![]() , 10分
, 10分
∴所求抛物线的方程为![]() ,双曲线的方程为
,双曲线的方程为![]() .··········· 12分
.··········· 12分
21.
原不等可化为 ![]() . 3分
. 3分
又 ![]() ,故
,故
①当![]() 或
或![]() 时,
时,![]() .则
.则![]() ;······································ 6分
;······································ 6分
②当![]() 时,
时,![]() .则
.则![]() ;············································· 8分
;············································· 8分
③当![]() 或
或![]() 时,不等式为
时,不等式为![]() 或
或![]() ,此时无解.·········· 10分
,此时无解.·········· 10分
综上:当![]() 或
或![]() 时,
时,![]() .则不等式的解集是
.则不等式的解集是![]() ;当
;当![]() 时,
时,![]() .则不等式的解集是
.则不等式的解集是![]() ;当
;当![]() 或
或![]() 时,不等式等价于
时,不等式等价于![]() 或
或![]() ,无解. 12分
,无解. 12分
22.
(Ⅰ) ∵H点坐标为(x,y),则D点坐标为(x,0),
由定比分点坐标公式可知,A点的坐标为(x,![]() y).
y).
∴![]() =(x+2,y),
=(x+2,y),![]() =(x-2,
=(x-2,![]() y).························································· 4分
y).························································· 4分
由BH⊥CA知x2-4+![]() y2=0,即
y2=0,即![]() +
+ ![]() =1,
=1,
∴G的方程为![]() +
+![]() =1(y≠0).·························································· 7分
=1(y≠0).·························································· 7分
(Ⅱ) 显然P、Q恰好为G的两个焦点,
∴![]() +
+![]() =4,
=4,![]() =2.
=2.
若![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() +
+![]() =
=![]() =1.
=1.
∴![]() ·
·![]() =
= ![]() +
+![]() =4.······················································ 11分
=4.······················································ 11分
由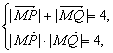 可得
可得![]() =
=![]() =2,
=2,
∴M点为![]() +
+![]() =1的短轴端点.
=1的短轴端点.
∴当M点的坐标为(0, ![]() )或(0,-
)或(0,-![]() )时,
)时,![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
············································································································· 14分