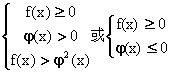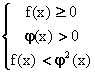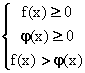第三单元 不等式的解法
[知识要点]
1、一元一次不等式ax>b
| 条件 | 解法或解集 | |
| a>0 | {xx> | |
| a<0 | {xx< | |
| a=0 | b³0 | xÎF |
| b<0 | bÎR | |
2、一元二次不等式ax2+bx+c>0(a¹0)
| 条件 | 解法或解集 | |
| D=b2-4ac>0 | 设方程ax2+bx+c=0的二根为x1,x2,且x1<x2 | |
| a>0 | {xx<x1或x>x2} | |
| a<0 | {xx1<x<x2} | |
| D= b2-4ac=0 | a>0 | {xxÎR,x¹ |
| a<0 | xÎF | |
| D= b2-4ac<0 | a>0 | xÎR |
| a<0 | xÎF | |
3、一元n次不等式
(x-α1)(x-α2)…(x-αn)<0,(x-α1)(x-α2)…(x-αn)>0.
| 条件 | 解法或解集 | |
| α1<α2<……<αn | 把α1,α2,…,αn按顺序标在数轴上,不等式的解区间如下 | |
| n为奇数 |
| |
| n为偶数 |
| |
4、分式不等式![]()
把α1,α2,…,αn与 β1,β2,…,βn按从小到大的顺序标在数轴上,解区间的确定同3.
5*、无理不等式
| 不等式 | 解法或解集 | |
|
| a³0 |
|
| a<0 | f(x)³0 | |
|
| a³0 |
|
| a<0 |
| |
| 不等式 | 解法或解集 | |
|
|
| |
|
|
| |
|
|
| |
[典型例题]
例1、解关于x的不等式ax2-(a+1)x+4>0
例2、解关于x的不等式mx2-2(m-1)x+(m+2)<0
例3、若不等式ax2+bx+c>0的解为α<x<β(α>0),求解不等式cx2-bx+a>0
例4、巳知不等式![]() 对所有实数x都成立,
对所有实数x都成立,
求q的取值范围。
例5、若不等式mx2-2x+1-m<0对满足-2£m£2的所有实数m都成立,求x的取值范围。
例6、若不等式x2-2mx+2m+1>0对满足0£x£1的所有实数x都成立,求m的取值范围。
例7、巳知满足关于x的不等式
p[x2-(p2+p+2)x+p3+2p2]£0的x的最大值为3,求p的值。
例8、若不等式组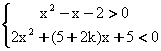 的整数解集为{-2},求实数k的取值范围。
的整数解集为{-2},求实数k的取值范围。
例9*、设函数f(x)=![]() ,其中a>0
,其中a>0
(1) 解不等式f(x)£1.
(2) 求a的取值范围,使函数f(x)在[0,+∞)上有单调性.
例10*、解关于x的不等式![]() .
.
例11*、解不等式![]() .
.
[测试题]
一、选择题
1、下列各组不等式中等价的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2、若f(x)表示-x+6与-2x2+4x+6二者中的较大者,则f(x)的解析式为( )
(A)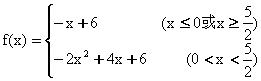 (B)
(B)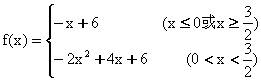
(C)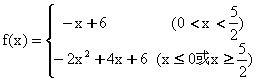 (D)
(D)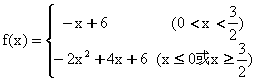
3、巳知a>1,则不等式![]() 的解集为( )
的解集为( )
(A)(-11,2) (B)(-∞,+∞) (C)F (D)与a有关的集合
4、不等式ax2+(ab+1)x+b>0的解集是1<x<2,则a和b的值为( )
(A)a=b=-1或a=b=-2 (B)a=-1,b=-![]() 或a=-2,b=-1
或a=-2,b=-1
(C)a=-![]() ,b=-1或a=-1,b=-2 (D)a=b=-
,b=-1或a=-1,b=-2 (D)a=b=-![]() 或a=b=-2
或a=b=-2
5、不等式![]() 的解集为( )
的解集为( )
(A)[3,5) (B)[1,3) (C)[1,5) (D){3}
二、填空题
6、巳知不等式(a+b)x+(2a-3b)<0的解为x<![]() ,则不等式(a-3b)x+(b-2a)>0的解集为
.
,则不等式(a-3b)x+(b-2a)>0的解集为
.
7、不等式![]() 的解集是
.
的解集是
.
8、不等式![]() 的解集为(4,b),则a=
.b= .
的解集为(4,b),则a=
.b= .
9、![]() ,则不等式
,则不等式![]() 的解集是
.
的解集是
.
三、解答题
10、解不等式(x-1)(x-2)(x-3)(x-4)>120
11、设A={xx2+3k2-1³2k(2x-1)},B={xx2-(2x-1)k+k2³0},则A![]() B,
B,
求k的取值范围。
12、关于x的不等式2x2-(2a+1)x+5>0在-1£x£1时恒成立,求a的取值范围。