高三数学单元测试题（一）
（不等式）
班级 姓名 座号 得分 .
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的, 每小题4分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
1．已知集合M={xx2<4}，N={xx2-2x-3<0}，则集合M
N=( )
A．
B．{xx＞3} C．{x－1＜x＜2
D．{x2＜x＜3
2．已知四个条件，①b＞0＞a ②0＞a＞b ③a＞0＞b ④a＞b＞0能推出
成立的有( )
A.1个 B.2个 C.3个 D.4个
3．设b＞a＞0，且a＋b＝1，则此四个数
，2ab，a2＋b2，b中最大的是( )
A.b
B.a2＋b2 Ｃ.2ab
D.
4．若x＞4，则函数
（ ）
A．有最大值—6 B．有最小值6 C．有最大值—2 D．有最小值2
5．函数
的最大值是（ B ）
A．
B．
C．
D．
6．不等式
的解集为
（ ）
A．（
，1）∪（1，
） B．（－∞，）∪（，+∞）
C．（－∞，1）∪（，+∞） D．（，1）∪（，+∞）
7．若x，y是正数，则
的最小值是（ ）
A．3 B．
C．4 D．
8．不等式 
的解集不是空集,则实数a的取值范围是（ ）
A．
B．
C．
D．
9．若函数
的定义域为R，则实数a 的取值范围是（ ）
A．
B．
C．
D．
10、已知实数x,y满足2x+y+5=0，那么
的最小值为（ ）
A．
； B．
； C．
； D．
二、填空题（把每小题的答案填在试卷对应题号的横线上。每小题5分共20分）
11、不等式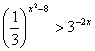
的解集是 .
12、不等式
的解集为 .
13．不等式
的解集不是空集，则实数a的取值范围是
。
14，已知
的最小值是 。
三、解答题：本大题共4小题，共40分，解答题写出文字说明、证明过程或演算步骤。
15、（10分）解不等式：
16．求函数
的定义域。（10分）
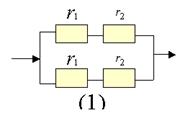
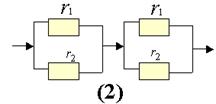17．如下图，已知是阻值不同的两个电阻 
、
，分别按图（1）和图（2）连接。设图（1）中的总阻值为
，图（2）中的总阻值为
，请判断、的大小，并加以证明。（10分）
18．（本小题满分10分）某工厂去年的某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元．今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入100万元（科技成本），预计产量年递增10万只，第n次投入后，每只产品的固定成本为
（k＞0，k为常数，
且n≥0），若产品销售价保持不变，第n次投入后的年利润为
万元．
（1）求k的值，并求出的表达式；
（2）问从今年算起第几年利润最高?最高利润为多少万元?
高三数学单元测试题（一）
一、选择题： C C A A B B C C B A
11.
, 12. 
13.a>1 14. 
15
解、原不等式等价于
（2分）
（4分） 
（7分）
或
（9分）
故原不等式的解集为：
或
。 （10分）
16．（1）a=0时，定义域为R。（2）a>0时，定义域为
（3）a〈0时，定义域为
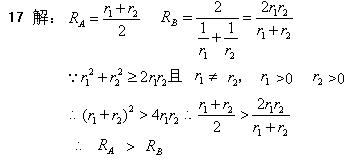
18.解：（1）由，当n＝0时，由题意，可得k＝8，
所以
．
（2）由
．当且仅当
，即n＝8时取等号，所以第8年工厂的利润最高，最高为520万元.