不等式练习2
一、选择题（每小题5分，总分60分）
1、不等式lgx2＜lg2x的解集是 （ ）
（A）（
，1）
（B）（100，＋∞）
（C）（，1）∪（100，＋∞）
（D）（0，1）∪（100，＋∞）
2、关于x的不等式（k2－2k＋
）x＜（k2－2k＋）1–x的解集是 （ ）
（A）x＞
（B）x＜ （C）x＞2
（D）x＜2
3、a＞1时，不等式x＋logax＜x＋logax的解集是 （ ）
（A）{x0＜x＜a｝ （B）{x0＜x＜1｝
（C）{xx＞0} （D）{xx＜0或x＞1}
4、不等式
＜2x＋a（a＞0）的解集是 （ ）
（A）{x0＜x≤a}
（B）{xx＞0或x＜－
}
（C）{x－
＜x＜a}
（D）{x－a≤x＜－或0＜x≤a }
5、已知不等式ax2＋bx＋2＞0的解集是{x－
}，则b－a的值等于（ ）
（A）－14 （B）－10 （C）10 （D）14
6、若不等式x2－logax＜0在（0，）内恒成立，则a的取值范围是 （ ）
（A）
≤x＜1 （B）＜a＜1 （C）0＜a≤ （D）0＜a＜
7、关于x的不等式ax2＋bx＋c＜0的解集为（－∞，
）∪（
，＋∞），其中＜＜0那么不等式cx2－bx＋a＞0的解集为 （ ）
（A）（－
）
（B）（
）
（C）（－
）
（D）（－∞，－
）∪（－，＋∞）
8、x
R时，不等式
恒成立，则实数a的取值范围是 （ ）
（A）0＜a＜1 （B）a＞
（C）0＜a＜ （D）a＜
9、若不等式x－2－x＋3＜a无解，则 （ ）
（A）a＞－5 （B）a≥－5 （C）a＜－5 （D）a≤－5
10、如果对于xR，不等式x＋1≥kx恒成立，则k的取值范围是 （ ）
（A）（－∞，0） （B）[－1，0]
（C）[0，1] （D）[0，∞）
11、若关于x的不等式x2－ax－
（A）－25≤a≤1 （B）a≤－25或a≥1
（C）－25≤a＜0或1≤a≤24 （D）－25≤a＜－24或0＜a≤1
12、设x1＜x2＜…xn，nN且n≥2，若{x（x－x2）（x－x3）…（x－xn）＞0}
{xx2－（x1＋xn）x＋x1xn＞0}，则n
（ ）
（A）等于2 （B）是大于2的任意奇数
（C）是大于2的任意偶数 （D）是大于1的任意自然数
二、填空题（每小题5分，总分30分）
1、设a＜0， －1＜b＜0， 则a、ab、ab2三者的大小关系是____________。
2、不等式
的解集为____________。
3、不等式log（x－1）（x2－1）＞1的解集为________________。
4、已知集合A＝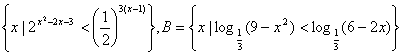
，
又A∩B＝{xx2＋ax＋b＜0}，则a＋b等于________.
5、关于x的不等式
的解集为
，则实数k的取值范围为____________.
6、不等式x2－3x＞4的解集为________________.
三、解答题（每小题12分，总分60分）
1、若x，y＞0，求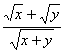
的最大值。
2、已知关于x的方程x2＋（m2－1）x＋m－2＝0的一个根比－1小，另一个根比1大，求参数m的取值范围。
3、解不等式：loga（x＋1－a）>1.
4、解不等式
.
5、已知函数f（x）＝ax2－c满足－4≤f（1）≤－1，－1≤f（2）≤5.
求证：－1≤f（3）≤20.
参考答案：
一、选择题
1、D 2、B 3、B 4、A 5、C 6、A 7、C 8、B
9、D 10、C 11、D 12、C
二、填空题
1、a＜ab2＜ab
2、{x－2＜x＜1}
3、{xx＞2}
4、－3.
5、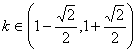
6、{xx＜－1或x＞4}
三、解答题
1、
2、－2＜m＜0
3、解：（I）当a>1时，原不等式等价于不等式组：
解得x>
（II）当0<a<1时，原不等式等价于不等式组：
解得：a－1<x<
综上，当a>1时，不等式的解集为{xx>
当0<a<1时，不等式的解集为{xa－1<x<
4、原不等价于不等式组（1）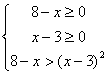
或（2）
由（1）得
， 由（2）得x＜3，
故原不等式的解集为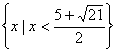
5、
，
，
，得－1≤f（3）＜20