浙江省龙游中学2006学年第二学期
高二数学第一次月考试卷 2006.3
一、选择题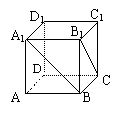
1.如图正方体中,直线![]() 与
与![]() 所成的角的大小为( C
)
所成的角的大小为( C
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.有6种不同的工作分配给6个人担任,每人只担任其中的一项工作,且有一人不能担任其中的某两项工作,则不同的分配方法有( B)
A.4![]() B.4
B.4![]() C.
C.![]() D.
D.![]()
3、在100件产品中,有3件是次品,现从中任意抽取5件,其中至少有2件次品的取法种数为 ( B )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4、n是奇数,二项式(1-x)2n+1展开式中系数最大的项是(C )
(A)第n项(B)第n+1项(C)第n+2项(D)第n+1,n+2项
5、二项式![]() 的展开式中,有理项共有( D )
的展开式中,有理项共有( D )
(A)3项 (B)5项 (C)6项 (D)7项
6.三个人坐在一排八个座位上,若每个人的左右两边都要有空位,则不同的坐法有(D)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在(x2+3x+2)5的展开式中,含x项的系数是(B )
A.160 B.240式 C.360 D.800
8.球面上有A、B、C三点,每两点间的线段AB=18,BC=24,AC=30,且球心到△ABC所在平面ABC的距离等于球半径的![]() ,那么球的表面积为 ( B )
,那么球的表面积为 ( B )
A.1600π B.1200π C.300π D.![]() π
π
9.式子![]() 的值为
( C
)
的值为
( C
)
![]() 124
124 ![]() 361
361 ![]() 124或361
124或361 ![]() 无法确定
无法确定
10.从装有白球3个、红球4个的箱子中,把球一个一个地取出来,到第五个恰好把白球全部取出的概率是 ( C )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
11.![]() 展开式中,常数项是
( A )
展开式中,常数项是
( A )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12.已知在6个电子元件中,有2个次品,4个合格品,每次任取一个测试,测试完后不再放回,直到两个次品都找到为止,则经过4次测试恰好将2个次品全部找出的概率( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.从0,1,2,…,9这10个数字中,选出3个数字组成三位数,其中偶数个数为( A )
(A)328 (B)360 (C)600 (D)720
14.从装有![]() 粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),设倒出奇数粒玻璃球的概率为
粒大小、形状相同但颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),设倒出奇数粒玻璃球的概率为![]() ,倒出偶数粒玻璃球的概率为
,倒出偶数粒玻璃球的概率为![]() ,那么( A )
,那么( A )
A、![]() B、
B、![]() C、
C、![]() D、以上都不对
D、以上都不对
二、填空题
15.若![]() 则
则
![]() 1
,
1
, ![]()
![]() 。
。
16. ![]() 展开式中含
展开式中含![]() 项系数为_____________。
项系数为_____________。
(法一)![]()
(法二)![]() 时
时
![]()
∴ 分子![]() 项系数为
项系数为![]()
∴ ![]() 的
的![]() 项系数为
项系数为![]()
17. 3个打字员为4家公司服务,每家公司各有一份文件要录入,则每个打字员都收到文件的概率为______4/9______.
(C
18.a.将正整数n表示成k个正整数的和(不计较各数的次序),称为将正整数n分成k个部分的一个划分,一个划分中的各加数与另一个划分的各加数不全相同,则称为不同的划分,将正整数n划分成k个部分的不同划分的个数记为![]() ,则
,则![]() =______8______.
=______8______.
b. 720能被_____24_______个不同的正偶数整除,所有这些正偶数的和为_____2340_______ (a、b二题任选一题)
三、解答题
19(本小题满分12分)6名同学站成一排:
①甲不站排头也不站排尾的不同排法有多少种?
②甲不站排头,且乙不站排尾的不同排法有多少种?
③甲、乙、丙不相邻的不同排法有多少种?
④甲、乙不相邻而且丙、丁也不相邻的排法有多少种?
解:①A![]() ·A
·A![]() =20×24=480(种) ②A
=20×24=480(种) ②A![]() -
-![]() +A
+A![]() =504(种)
=504(种)
③A![]() ·A
·A![]() =144(种)
=144(种)
④法1:
则![]()
解得![]()
法2:排法数=![]() -甲、乙相邻排法数-丙、丁相邻排法数+甲、乙相邻且丙、丁相邻排法数
-甲、乙相邻排法数-丙、丁相邻排法数+甲、乙相邻且丙、丁相邻排法数
即![]() =336
=336
法3:![]() ( 用插入法,分二类插)
( 用插入法,分二类插)
法4:甲、乙不相邻-甲、乙不相邻且丙、丁相邻
20.已知集合![]() ,
,![]() 是
是![]() 到
到![]() 的映射,
的映射,
(1)若![]() 中每一个元素都有原象,这样不同的映射
中每一个元素都有原象,这样不同的映射![]() 有多少个?
有多少个?
 (2)若
(2)若![]() 中元素0必无原象,这样的映射
中元素0必无原象,这样的映射![]() 有多少个?
有多少个?
(3)若![]() 满足
满足![]() ,这样的映射
,这样的映射![]() 有多少个?
有多少个?
解(1)![]() (2)
(2)![]() (3)
(3)![]()
法2:![]() =
=![]() =
=![]() =
=![]()
有![]() =31
=31
21.(本小题满分14分)
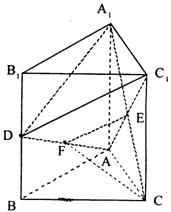
(理科学生做)如图,已知正三棱柱ABC- ![]() ,D是AC的中点,∠
,D是AC的中点,∠![]() DC = 60°
DC = 60°
(Ⅰ)求证:AB1∥平面B![]() D;
D;
(Ⅱ)求二面角D-B![]() -C的大小。
-C的大小。
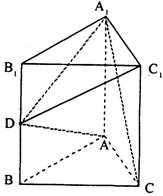 (文科学生做)如图,直三棱柱ABC-
(文科学生做)如图,直三棱柱ABC-![]() ,AB =
AC = 1,AA
,AB =
AC = 1,AA![]() = 2,∠
= 2,∠![]() = 90°,D为BB
= 90°,D为BB![]() 的中点。
的中点。
(Ⅰ)求证:AD⊥平面A![]() DC1;
DC1;
(Ⅱ)求异面直线C![]() D与直线A
D与直线A![]() C所成角的余弦值。
C所成角的余弦值。
解.(理科)
(Ⅰ)连结B交BC![]() 于O,则O是B
于O,则O是B![]() C的中点,连结DO。
C的中点,连结DO。
∵在△A![]() C中,O、D均为中点,
C中,O、D均为中点,
∴A![]() ∥DO…………………………3分
∥DO…………………………3分
∵A![]()
![]() 平面B
平面B![]() D,DO
D,DO![]() 平面B
平面B![]() D,
D,
∴A![]() ∥平面B
∥平面B![]() D。…………………6分
D。…………………6分
(Ⅱ)设正三棱柱底面边长为2,则DC = 1。
∵∠![]() DC = 60°,∴C
DC = 60°,∴C![]() =
= ![]() 。
。
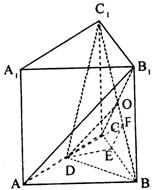 作DE⊥BC于E。
作DE⊥BC于E。
∵平面BC![]() ⊥平面ABC,
⊥平面ABC,
∴DE⊥平面BC![]()
![]()
作EF⊥B![]() 于F,连结DF,则 DF⊥B
于F,连结DF,则 DF⊥B![]()
∴∠DFE是二面角D-B![]() -C的平面角……………10分
-C的平面角……………10分
在Rt△DEC中,DE=![]()
在Rt△BFE中,EF = BE·sin![]()
∴在Rt△DEF中,tanDFE = ![]()
∴二面角D-B![]() -C的大小为arctan
-C的大小为arctan![]() ………………………14分
………………………14分
(文科)解法一:
(Ⅰ)∵A![]() ⊥平面
⊥平面![]() ,
,
 ∴AA1⊥A1
∴AA1⊥A1![]()
又![]() C1⊥
C1⊥![]()
![]() ,
,
∴A1![]() ⊥平面
⊥平面![]()
![]() BA
BA
∴AD⊥![]()
![]()
∵AD =![]() ,
,![]() D =
D =![]() , A
, A![]() = 2,
= 2,
由此![]() ,
,
得![]() D⊥AD
D⊥AD
∵![]()
![]() ∩
∩![]() D =
D = ![]()
∴AD⊥平面![]() D
D![]() ……………………7分
……………………7分
(Ⅱ)连结A![]() 交
交![]() C于点E,取AD的中点F,连结EF,则EF∥
C于点E,取AD的中点F,连结EF,则EF∥![]() D
D
∴∠CEF或它的补角就是异面直线![]() D与直线
D与直线![]() C所成的角
C所成的角
由(Ⅰ)知,AD⊥![]()
![]() ,则AD⊥AC,又AF =
,则AD⊥AC,又AF = ![]() AD =
AD =![]() 在△CEF中,
在△CEF中,
CE =![]() ,EF =
,EF =![]() ,CF =
,CF =![]()
cos CEF =![]()
![]()
则异面直线![]() D与直线
D与直线![]() C所成角的余弦值为
C所成角的余弦值为![]() …………14分
…………14分
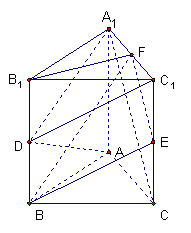 法2:取CC1及A
法2:取CC1及A
![]() ,
,![]() ,
,![]() =
=![]()
=![]() ,所以
,所以![]()
![]() =
=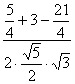
=![]()
![]()
所以异面直线![]() D与直线
D与直线![]() C所成角的余弦值为
C所成角的余弦值为![]()
22.(12分)把4个不同的球任意投入4个不同的盒子内(每盒装球数不限),
计算(1)无空盒的概率;(2)恰有一个空盒的概率.
解:4个球任意投入4个不同的盒子内有44种等可能的结果.
(1)其中无空盒的结果有![]() 种,所求概率:P=
种,所求概率:P=![]()
答:无空盒的概率是![]() .
.
(2)先求恰有一空盒的结果数:选定一个空盒有![]() 种,选两个球放入一盒有
种,选两个球放入一盒有![]() 种,其余两球放入两盒有
种,其余两球放入两盒有![]() 种,故恰有一个空盒的结果数为:
种,故恰有一个空盒的结果数为:![]()
![]() ,所求概率:
,所求概率:
P(A)=![]()
答:恰有一个空盒的概率是![]() .
.
23.(12分) 已知:![]() 的展开式中,各项系数和比它的二项式系数和大
的展开式中,各项系数和比它的二项式系数和大![]() .
.
(1)求展开式中二项式系数最大的项;(2)求展开式中系数最大的项。
解:令![]() ,则展开式中各项系数和为
,则展开式中各项系数和为![]() ,又展开式中二项式系数和为
,又展开式中二项式系数和为![]() ,
,
∴![]() ,
,![]() .
.
(1)∵![]() ,展开式共
,展开式共![]() 项,二项式系数最大的项为第三、四两项,
项,二项式系数最大的项为第三、四两项,
∴![]() ,
,![]() ,
,
(2)设展开式中第![]() 项系数最大,则
项系数最大,则![]() ,
,
∴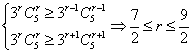 ,∴
,∴![]() ,
,
因此展开式中系数最大的项为![]()
已知(![]() +3x2)n展开式中各项的系数和比各项的二项式系数和大992,求(1)展开式中系数最大的项.(2)当
+3x2)n展开式中各项的系数和比各项的二项式系数和大992,求(1)展开式中系数最大的项.(2)当![]() 时展开式中第几项的值最大.
时展开式中第几项的值最大.
策略:由系数间的关系可求n,然后求系数最大的项即求系数不小于其前一项和后一项的系数的项,可以列不等式组求解.
解:令x=1,得各项的系数和为(1+3)n=4n,而各项的二项式系数和为![]() +
+![]() +…+
+…+![]() =2n,∴4n=2n+992
=2n,∴4n=2n+992
∴2n=32或2n=-31(舍)
∴n=5,设第r+1项系数最大,则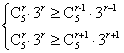 即
即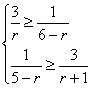
∴![]() ≤r≤
≤r≤![]() ,又r∈Z ∴r=4
,又r∈Z ∴r=4
∴系数最大的项是第五项,且T5=![]() .
.
评注:本思想方法不仅适用于求系数最大(小)项问题,在数列问题中也广泛采用.