直线与平面垂直

数学单元测试题（直线与平面垂直）学号　　 姓名 　　　　　　　　　

一．选择题：

1．若平面α外两直线a,b在α上的射影是两相交直线，则a与b的位置关系是　 （　　 ）

　A  相交　　　　 B 相交或异面　　 C 异面　　　　　 　 D 相交或平行

2．已知P是△EFG所在平面外一点，且PE=PG，则点P在面EFG上的射影一定在（　　 ）

　A .∠FEG的平分线上　　　　 B. 边BG的高上

 C. 边EG的中线上 　　　　　 D. 边EG的垂直平分线上

3．已知直线a, b和平面α，下列推论错误的是(　　)

　（A）　　　　　（B）

　（C） 　 （D）

4．直线a⊥b，且a//平面α，则b与α的位置关系是

　（A）bα  （B）bα　（C）b//α或bα （D）b与α相交或b//α或bα

5．若a, b是异面直线，那么经过b的所有平面中　 (　　 )

　（A）只有一个平面与α平行　（B）只有一个平面与α垂直

　（C）有无数个平面与α平行　（D）有无数个平面与α垂直

6．正方体ABCD—A₁B₁C₁D₁中，AC₁与B₁C所成的角是(　 )

　（A）30°  （B）45°　（C）60°  （D）90°

7．正方形ABCD的边长为12cm，PA⊥平面AC，且PA=12cm，则点P到BD的距离为（　　 ）

　A .　　　　  B.　 　　　　C.　 D .

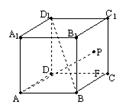8．如图，正方体ABCD－A₁B₁C₁D₁中，点P在侧面BB₁C₁C及其面界上运动，并且保持AP⊥BD₁，则动点P的轨迹是(　　)

　（A）线段B₁C　　　　　　 （B）线段BC₁

　（C）BB₁中点与CC₁中点连成的线段

（D）BC中点与B₁C₁中点连成的线段

9. 正方体ABCD—A₁B₁C₁D₁中，M, N, P分别是棱A₁B₁, DD₁, BC的中点，则AN与PM所成的角是(　 )

　（A）30°  （B）45°　（C）60°  （D）90°

二．填空题：

10．P为△ABC所在平面外一点，O为P在平面ABC上的射影（1）若P到△ABC三边距离相等，且O在△ABC内部，则点O是△ABC的　　　　心；（2）若PA⊥BC, PB⊥AC, PC⊥AB，则点O是△ABC的　　　　　 心；

11．正三角形ABC边长为a，AD⊥BC于D，沿AD把△ABD折起，使∠BDC=90°，这时A到BC的距离为　　　　　  .

三．解答题：

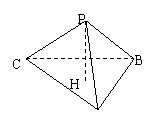
12．如图，已知H为△ABC的垂心，PH⊥平面ABC，且∠APB=90⁰，求证：PC⊥PB。

13． 在矩形ABCD中，AB=1，BC= a,P是平面ABCD外的一点，且PA=1。

请问：BC边上是否一定存在点Q，使得？为什么？

13、如图，正方体ABCD－A₁B₁C₁D₁中，E为A₁B₁的中点，O是B₁C与BC₁的交点。

求证：DO面EBC₁

12．P是△ABC所在平面外一点，若P在平面ABC内射影是△ABC的垂心，求证：A在平面PBC上的射影也是△PBC的垂心。

13、如图，P是△ABC所在平面外一点，PA=PB，CB⊥平面PAB，M是PC的中点，N是AB上的点，AN=3NB，

　 （1）求证：MN⊥AB；

　 （2）当∠APB=90°，BC=2，AB=4时，求MN的长。

16．在正方体ABCD-A₁B₁C₁D₁中，求证：

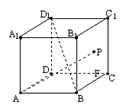(1)正方体对角线AC₁⊥面对角线B₁C；

(2)AC₁⊥截面CB₁D。

12．在棱长为a的正方体ABCD－A₁B₁C₁D₁中，E为CC₁的中点，求点E到A₁B的距离。