职业中专数学期中考试题

高二对口班月考数学试卷

班级　　　　姓名　　　　　 　记分　　　　 

 

一、　　选择题：（每小题4分，共60分）

1.C₅¹+C₅²+C₅³+C₅⁴的值等于(　　 )

A.30　　　　　　 B.31　　　　　　 C.32　　　　　　 D.33

2．某学生通过英语测试的概率为，他连续测试3次，那么其中恰有一次获得通过的概率是（ 　 ）

A．　　 　　　　 B．　　　　　　　　C．　　　　　　　　　 D．

3．甲、乙、丙、丁四个建筑队承包五项不同的工程，每个队至少承包一项工程，那么甲队承包两项工程的概率为（　　 ）

A．　　　　　　　　B．　　　　　　　　 C．　　　　　　　　　　　D．

4．从7人中选派5人到10个不同交通岗的5个中参加交通协管工作，则不同的选派方法有（　　 ）

　　　A、种　　　 B、种　　  C、种　　 D、

5、在处的导数是　(　　　)

A. 0　　　　　  B.　1　　　　　 C.　3　　　　　  D.　6

6.有甲、乙、丙三项任务，甲需2人承担，乙、丙各需1人承担 ，从10人中选派4人承担这三项任务，不同的选择共有(　　 )

A.1260种　　　 　B.2025种　　  　C.2520种　　  　D.5040种

7.的展开式中项的系数是(　　 )

A 840　　　　　　　　　　　　　　　　B  　　　　　　　　　　　　　C 210　 　　　　D

8. 某人射击一次击中的概率为0.6,经过3次射击,此人至少有两次击中目标的概率（　）

　　　A． 　　　　　　 B．　　　　 C． 　　　　　D．

9．曲线在点（1，1）处的切线方程是（　　）

　　A．　　　 B．

　　C．x-2y+1=0　　　　　　　　 D．x+2y+1=0

10．下列结论不正确的是（　　 ）

　　A．若y=3，则y′=0　　　　　　  B．若，则。

C．若，则　 　　　D．若y=3x，则。

11．曲线在x=2处的导数为12，则n的值为（　　 ）

　　A．1　　　　　 B．2　　　　 C．3　　　　  D．4

12．　　　　　　　 10x　　 x>1

  若f(x)=　　5　　　  x=1　　　　则 的值为　　　 （　 ）

7-x　 　 x<1

A． 5　　　　 B. 6　　　　  C. 10　　　　　 D. 不存在

13.下列命题不正确的是（ 　 ）
A．如果 f (x) = ，则 f (x) = 0　　　　　　　

B．如果 f (x) = 2 ^x－1，则 f (x) = 0　　　　　　　　
C．如果 f (n) = ，则 f (n) 不存在

D．如果 f (x) = ，则 f (x) = 0

14 已知f(x)=sin, 则f′(x)=　(　　)

　　　　　　　　　　　　　 　　　　　　　

A  　　　　　　　　　B  -

C  　　　　　　　　　D  -

15下列求导运算正确的是(　　 )

　　　　　　　　　　　　　　　　　　　　　　　　

A  (x+　　　　　　　  B　(log₂x)′=　

　　　　  C　(3^x)′=3^xlog₃e　　　　　　  D　(x²cosx)′=-2xsinx

二、填空题：（每小题5分，共30分）

16、3名男生和4名女生站成一排，如果男生必须相邻，有　　　　种站法；如果男生都不相邻，有　　　　种站法.（用数字作答）

17、若10把钥匙中只有2把能打开某锁，则从中任取2把能将该锁打开的概率为________。

18、 的展开式中，常数项为　　　　 。（用数字作答）

19、函数的导数是________________。

20、在一次三人象棋对抗赛里，甲胜乙的概率为0.4，乙胜丙的概率为0.5，丙胜甲的概率为0.6，比赛顺序如下：第一局，甲对乙；第二局，第一局的胜者对丙；第三局，第二局的胜者对第一局的败者；第四局，第三局的胜者对第二局的败者。则乙连胜四局的概率为　　　　   。

21、若曲线y=2x²在点P处的切线的斜率等于4，则点P的坐标为  　　　　 。

三、解答题：（60分）

22、从6个数字0，1，2，3，4，5中，每次取出5个不同的数字，问：

　 （1） 可以组成多少个不同的五位数？ （2）1在首位，5在末位的五位数由多少个？

（3）5的倍数有多少个？（每小问4分，共12分）

23、计算题：（20分）

求极限：　　　　　　　　　　　

求导数：  （1）y=(2x²-5x+2)e^x （2）　y = lncos2x ,（在x = ）

24、甲、乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被乙独立解出的概率为0.8。

（1）求该题被解出的概率；（6分） （2）求解出该题的人数X的期望与方差。（6分）

25、已知函数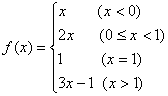，问f(x)在x=0和x=1处的极限是否存在？是否连续？

（8分）

26、曲线在点A处的切线的斜率为3，求该曲线在A点处的切线方程。

（8分）

答案：

一：选择题：

题号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
答案	A	C	D	D	D	C	A	A	C	B	C	B	D	D	D

二：填空题：

16 、780　 1440　； 17、  ； 18、70　；  19、  ；

 20 、0.09　； 21 、  （1，2）。

三：解答题：

22、 600 ，24 ， 216 。

23、

求极限

（分子、分母同除以x²）

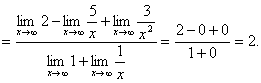
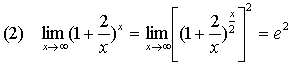
求导数

 　

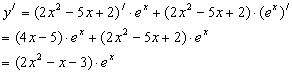
(2)

　

24、（1）0.92 （2）1.4　0.4

25、解：∵，∴.

又f(0)=0，∴f(x)在x=0处连续，

∵，

∴，

又f(1)=1， ∴f(x)在x=1处不连续.

26、由导数定义求得，

　　令，则x=±1。

　　当x=1时，切点为（1，1），所以该曲线在（1，1）处的切线方程为y-1=3(x-1)即3x-y-2=0；

　　当x=-1时，则切点坐标为（-1，-1），所以该曲线在（-1，-1）处的切线方程为y+1=3(x+1)即3x-y+2=0。