重庆市万州区高2007级高二上数学综合训练题
班级 姓名 学号______________
(全卷共三个大题,共22个小题,满分150分,时间120分钟)
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一、选择题(本大题共10个小题,每小题5分,共50分)在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母代号填在题后括号内.
1.不等式![]() 的解集为( )
的解集为( )
A.(0,2)
B.![]()
C.(-4,0)
D. ![]()
2. 不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若![]() 满足
满足![]() ,则直线
,则直线![]() 必过定点( )
必过定点( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
4.焦点为![]() ,且与双曲线
,且与双曲线![]() 有相同的渐近线的双曲线方程是( )
有相同的渐近线的双曲线方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.过双曲线![]() 左焦点F1的弦AB长为6,则
左焦点F1的弦AB长为6,则![]() (F2为右焦点)的周长是( )
(F2为右焦点)的周长是( )
A.28 B.22
C.14 D.12
6.设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )
A.[-![]() ,
,![]() ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
7.双曲线的两条准线将实轴三等分,则它的离心率为( )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
8.设![]() ,则
,则![]() 的最小值是(
)
的最小值是(
)
A. 1 B. 2 C. 3 D. 4
9.在椭圆![]() 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使MP+2MF的值最小,则这一最小值是( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使MP+2MF的值最小,则这一最小值是( )
A.![]() B.
B.![]() C.3 D.4
C.3 D.4
10.已知椭圆![]() ( a > b > 0) 的离心率为
( a > b > 0) 的离心率为![]() ,准线为
,准线为![]() 、
、![]() ;双曲线
;双曲线![]() 离心率为
离心率为![]() ,准线为
,准线为![]() 、
、![]() ;;若
;;若![]() 、
、![]() 、
、![]() 、
、![]() 正好围成一个正方形,则
正好围成一个正方形,则![]() 等于( )
等于( )
A. ![]() B .
B .![]() C.
C.![]() D.
D. ![]()
二、填空题(本大题共6小题,每小题4分,共24分)请把正确答案直接填写在题中的横线上.
11. 不等式 ![]() 的解集是____________________________.
的解集是____________________________.
12. 圆![]() 对称的圆的方程是___________________.
对称的圆的方程是___________________.
13.设![]() 满足约束条件:
满足约束条件: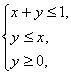 则
则![]() 的最大值是__________________.
的最大值是__________________.
14.经过两条直线![]() 和
和![]() 的交点,且与向量
的交点,且与向量![]() 垂直的直线方程为_____________________________ .
垂直的直线方程为_____________________________ .
15.F1,F2是双曲线![]() 的两个焦点,P是双曲线上的点,已知PF1,PF2,F1F2依次成等差数列,且公差大于0,则∠F1PF2=
.
的两个焦点,P是双曲线上的点,已知PF1,PF2,F1F2依次成等差数列,且公差大于0,则∠F1PF2=
.
16.设有五个条件:①平面γ与平面α 、β所成的锐角相等; ②直线a∥b,a⊥平面α ,
b⊥平面β;③a、b是异面直线,![]() ;④平面α内距离为d的两条平行线在平面β内的射影仍为两条距离为d的平行线;⑤平面α内有不共线的三点到平面β的距离相等.其中能推出平面α∥β的条件有_____________.(填写所有正确条件的代号)
;④平面α内距离为d的两条平行线在平面β内的射影仍为两条距离为d的平行线;⑤平面α内有不共线的三点到平面β的距离相等.其中能推出平面α∥β的条件有_____________.(填写所有正确条件的代号)
三、解答题(本大题共6小题,共76分)解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分13分)
已知:a,b,c,d都是实数,且a2+b2=1,c2+d 2=1.
求证:|ac+bd|≤1.
18.(本小题满分13分)
求经过点A(2,-1),和直线![]() 相切,且圆心在直线
相切,且圆心在直线![]() 上的圆的方程.
上的圆的方程.
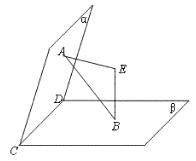
19.(本小题满分12分)
已知二面角α-CD-β的大小为60°,EA⊥平面α,垂足为A,EB⊥平面β,垂足为B,EA=3,EB=4.
(1)求证:CD⊥AB;
(2)求E到CD的距离.
| |
某村计划建造一个室内面积为800![]() 的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1
的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1![]() 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3![]() 宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大.最大种植面积是多少?
宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大.最大种植面积是多少?
21.(本小题满分12分)
已知:抛物线![]() 的一条焦点弦被焦点分成长为m、n的两部分.
的一条焦点弦被焦点分成长为m、n的两部分.
求证:![]() 为定值.
为定值.
22.(本小题满分14分)
已知动点![]() 与双曲线
与双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 的距离之和为定值,且
的距离之和为定值,且![]()
![]() 的最小值为
的最小值为![]() .
.
(I)求动点![]() 的轨迹方程;
的轨迹方程;
(II)若已知![]() ,
,![]() 、
、![]() 在动点
在动点![]() 的轨迹上且
的轨迹上且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(期末综合训练题)参考答案
一、选择题(每小题5分,共50分)
1~5 DA B B A 6~10 C B C C A
二、填空题(每小题4分,共24分)
11. ![]() ;12.
;12. ![]() ;13.2;
;13.2;
14. ![]() ;15. 120°;16. ②③.
;15. 120°;16. ②③.
三、解答题(6个小题,共76分)
17. (本小题满分13分)
证明:∵a2+c2≥2ac,b2+d2≥2bd,
∴a2+b2+c2+d2≥2(ac+bd),
∴ac+bd≤![]() =1.
……………………5分
=1.
……………………5分
又∵a2+c2≥-2ac,b2+d2≥-2bd,
∴a2+b2+c2+d2≥-2(ac+bd),
∴ac+bd≥-![]() =-1.
……………………10分
=-1.
……………………10分
∴ac+bd≤1. ………………13分
18. (本小题满分13分)
解:因为圆心在直线![]() 上,因此可设圆心坐标为
上,因此可设圆心坐标为![]() ,由题意:
,由题意:
![]() ……………………3分
……………………3分![]() ……………………8分
……………………8分
所以圆心坐标为![]() ,半径为
,半径为![]() , ……………………10分
, ……………………10分
从而所求圆的方程为:![]()
即是:![]() ……………………13分
……………………13分
19. (本小题满分12分)
(1)证明: ![]() ……………………………………………… 2分
……………………………………………… 2分
同理CD⊥EB
![]() ,∴CD⊥面AEB,
,∴CD⊥面AEB,![]() …………… 4分
…………… 4分
(2)解:设CD与面AEB交于O,连OA,OB
![]()
∠AOB=60° ………………………………………6分
OE是E到CD的距离.
∠EAO+∠EBO=180°, A、O、B、E四点共圆,∠AEB=120°……………… 8分
△AEB中,![]()
![]()
AB=![]() . ……………………………………………………10分
. ……………………………………………………10分
![]() ……… 12分
……… 12分
20. (本小题满分12分)
解:设矩形温室的左侧边长为![]() ,后侧边长为
,后侧边长为![]() ,则
,则![]() ……………1分
……………1分
蔬菜的种植面积 ![]() ……………………6分
……………………6分
所以 ![]() ……………………8分
……………………8分
当![]() ………………11分
………………11分
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648m2. ……………………12分
21. (本小题满分12分)
解:由题可知,焦点坐标为(1,0)
当焦点弦AB与对称轴垂直时,![]()
![]() ………………………4分
………………………4分
当焦点弦AB与对称轴不垂直时,设其方程为![]()
将其代入抛物线![]()
有![]() …………………………6分
…………………………6分
令![]()
则![]()
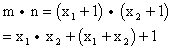
![]() ………………10分
………………10分
![]() ,即
,即![]()
综上可知![]() 为定值.
………………12分
为定值.
………………12分
22. (本小题满分14分)
解:(I)由题意![]() ,设
,设![]() (
(![]() ),由余弦定理, 得
),由余弦定理, 得
![]() .……………………2分
.……………………2分
又![]() ·
·![]() ,
,
当且仅当![]() 时,
时,![]() ·
·![]() 取最大值,……………………4分
取最大值,……………………4分
此时![]() 取最小值
取最小值![]() ,令
,令![]() ,解得
,解得
![]() ,
,![]() ,∴
,∴![]() ,故所求
,故所求![]() 的轨迹方程为
的轨迹方程为![]() .…………6分
.…………6分
(II)设![]() ,
,![]() ,则由
,则由![]() ,可得
,可得
![]() ,故
,故![]() ,……………………8分
,……………………8分
∵![]() 、
、![]() 在动点
在动点![]() 的轨迹上,故
的轨迹上,故![]() 且
且![]() ,
,
消去![]() 可得
可得![]() ,解得
,解得![]() ,……………………12分
,……………………12分
又![]() ,∴
,∴![]() ,解得
,解得![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .……14分
.……14分