襄樊市高中调研测试题(2006.1)

高二数学(理科)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟．

第 Ⅰ 卷(选择题，共60分)

注意事项：

1．请考生将自己的学校、班级、姓名、考号填写在第Ⅱ卷密封线内．

2．每小题选出答案后在第Ⅱ卷前的答题栏内用2B铅笔把对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题上．

一．选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)

1.　不等式≥0的解集是
　　A．{x｜x≥－2}　　　　　　　　　　　　　　　　　　　　　B．{x｜x＞－2或x≤－2}
　　C．{x｜－2≤x<－1}　　　　　　　　　　　　　　　　　 D．{x｜－2≤x<－1或x＞－1}

2.　若a＞b＞c, 则下列不等式一定成立的是
　　　A．ab＞ac　　　　　　　　　　　　　　　　　　　　　　　 B．a c ＞b c
　　　C． ab ＞ bc 　　　　　　　　　　　　　　　　　　　D．a (b＋c)＞c(b＋c)

3.　　不等式a＞b和同时成立的充要条件是
　　A．a＞b＞0　　　　　　　 B．a＞0＞b　　　　　　　 C．　　　　　 D．

4.　　在下列函数中，最小值为4的函数是
　　A．　　　　　　　　　　　　　　　　　　　　　　　B．
　　C．　　　　　　　　　　　　　　　　　　　　　D．

5.　　如果直线与圆有两个不同的交点，则点P (a，b)与圆的位置关系是
　　A．点P在圆外　　　　　　　　　　　　　　　　　　　　　 B．点P在圆上
　　C．点P在圆内　　　　　　　　　　　　　　　　　　　　　 D．点P与圆的位置关系不定

6.　　不等式│x²－2│＜1的解集为
　　A．{x│－1＜x＜　　　　　　　　　　　　　　　　　 }　　　　　　　　　　　　　　　　B．{x│－1＜x＜1或x＞}
　　C．{x│＜x＜－1或1＜x＜}　　　　 D．{x│x＜1或1＜x＜}

7.　　点P(1，0)到曲线 (其中参数t∈R)上的点的最短距离为
　　A．0　　　　　　　　　　　　　B．1　　　　　　　　　　　　　C．　　　　　　　　　　　D．2

8.　　△ABC 三个顶点为A(2，4)、B(－1，2)、C(1，0)，点P(x，y)在△ABC内部及边界运动，则的最大值及最小值分别是
　　A．3，1　　　　　　　　　　 B．－1，－3　　　　　　　C．1，－3　　　　　　　　 D．3，－1

9.　　现用铁丝做一个面积为1平方米、形状为直角三角形的框架，有下列四种长度的铁丝各一根供选择，其中最合理(即够用，浪费最少)的一根是
　　A．4.6米　　　　　　　　　 B．4.8米　　　　　　　　　 C．5.0米　　　　　　　　　 D．5.2米

10. 曲线的离心率为
　　A.　　　　　　 B.　　　　　　　　　　　　　C.2　　　　　　　　D．不确定

11. 一个酒杯的轴截面是抛物线的一部分，它的方程是(0≤y≤20)，在杯内放一个玻璃球，要使球触及酒杯底部，则玻璃球的半径r的取值范围是
　　A．0＜r≤1　　　　　　　　B．0＜r＜1　　　　　　　　C．0＜r≤2　　　　　　　　D．0＜r＜2

12. 已知两点M(－5，0)和N (5，0)，若直线上存在点P使，则称该直线为“B型直线”．现给出下列直线：①；②y = 2；③；④．其中“B型直线”有
　　A．1条　　　　　　　　　　　B．2条　　　　　　　　　　　C．3条　　　　　　　　　　　D．4条

第Ⅰ卷答题栏

[ A ]

[ B ]

[ C ]

[ D ]

襄樊市高中调研测试题(2006.1)

高二数学(理科)

第 Ⅱ 卷(非选择题，共90分)

注意事项：

第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．

题号	一	二	三						总　分
题号	一	二	17	18	19	20	21	22	总　分
得分

得分	评卷人

二．填空题(本大题共4小题，每小题4分，共16分．将正确答案填在题中横线上)

13. 已知定点A(0，1)，点B在直线上运动，当线段AB最短时，点B的坐标是_____________________．

14. 光线从点M(－2，3)射到x轴上一点P (1，0)后被x轴反射，则反射光线所在的直线方程为___________________．

15. 曲线的准线与y轴平行，则实数k的取值范围为_____________________．

16. 定义符号函数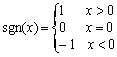，则不等式的解集为_________________________．

三．解答题(本大题共6小题，满分74分．解答应写出文字说明，证明过程或演算步骤)

得分	评卷人

17.　 (本大题满分12分)圆C过点(2，－1)，圆心在直线上，且与直线相切，求圆C的方程．

得分	评卷人

18.　 (本大题满分12分)已知集合M＝，集合N＝，求集合．

19.　 (本大题满分12分)
(1)已知a、b是正数，a≠b，x、y∈(0，+∞)，求证：≥．
(2)利用(1)的结论求函数的最小值，并指出取得最小值时的x值．

得分	评卷人

20.　 (本大题满分12分)某厂为适应市场需求，投入98万元引进先进设备，并投入生产，第一年需各种费用12万元，从第二年开始，每年所需费用会比上一年增加4万元，每年因引进该设备可获得年利润50万元．请你根据以上数据，解决以下问题：
　　(1)引进该设备多少年后，开始盈利？
　　(2)引进该设备若干年后，有两种处理方案：第一种：年平均利润达到最大值时，以26万元的价格卖出该设备；第二种：盈利达到最大值时，以8万元的价格卖出该设备．问哪种方案较为合算？

得分	评卷人

21.　 (本大题满分12分)已知抛物线的准线与轴交于M点，过M点的直线l与抛物线交于A、B两点，若线段AB的垂直平分线与x轴交于D (x₀，0)．
　　(1)求x₀的取值范围；
　　(2)△ABD能否是正三角形？若能求出x₀的值，若不能，说明理由．

得分	评卷人

22.　 (本大题满分14分)有对称中心的曲线叫做有心曲线，显然椭圆、双曲线都是有心曲线．过有心圆锥曲线的中心的弦叫有心圆锥曲线的直径．

定理：过圆上异于直径两端点的任意一点与一条直径的两个端点连线，则两条连线的斜率之积为定值－1．
　　(1)写出定理在椭圆中的推广，并加以证明；
　　(2)写出定理在双曲线中的推广；你能从上述结论得到有心圆锥曲线(包括椭圆、双曲线、圆)的一般性结论吗？请写出你的结论．

得分	评卷人

襄樊市高中调研测试题(2006.1)

高二数学(理科)参考答案及评分标准

说明：

　　　 1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．

　　　 2．对计算题当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．

　　　 3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．

4．只给整数分数，选择题和填空题不给中间分数．

一．选择题：

DDBC　　ACBC　　CCAB

二．填空题：

13．　　14．y = x－1　　15．(－∞，0)(1，＋∞)　　16．{x｜－4<x＜2}

三．解答题：

17．解：∵圆心在直线2x＋y＝0上，∴设圆心为(t，－2t)　　　　　　　　　　　　　　　　　2分
　　则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分
　　即，解得：t = 1或t = 9　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 6分
　　当t = 1时，，圆心为(1，－2)
　　当t = 9时，，圆心为(9，－18)　　　　　　　　　　　　　　　　　　　　　8分
　　∴圆的方程为或　　　　　　　　　　　　　12分

18．解：由得：－2＜x＜－1或4＜x＜7
　　∴M = {x｜－2＜x＜－1或4＜x＜7}　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分
　　令，则化为，即t²＋2at－3a²＞0　　　　　　　　　 6分
　　解得t＞a或t＜－3a(舍去)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分
　　∴，故　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分
　　由得：a＜7，∴T = {a｜0＜a＜7}　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

19．(1)证法一：
　　∵ a、b是正数，x、y∈(0，+∞)，∴≥0
　　∴≥
　　当且仅当bx－ay = 0，即时，“＝”成立．　　　　　　　　　　　　　　　　　　　　　　　6分

证法二：
　　　　　　≥
　　∵ a、b是正数，x、y∈(0，+∞)，∴≥
　　当且仅当，即时，“＝”成立．　　　　　　　　　　　　 6分

(2)解：∵，∴
　　由(1)知　　　　　　　　　　　　　　　　　8分
　　　　　　　 ≥　　　　　　　　　　　　　　　　　　　　 10分
　　当且仅当，即时，上式取“＝”
　　∴当时，函数f (x)有最小值25．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

20．(1)解：设引进该设备x年后开始盈利，盈利额为y万元
　　x年中所需费用为　　　　　　　　　　　　　　　　　　　　　　　　　2分
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分
　　令y＞0得：
　　由于x是整数，∴3≤x≤17
　　∴引进该设备3年后开始盈利　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分

(2)解：第一种方案：年平均盈利为
　　当且仅当，即x = 7时年平均利润最大，共盈利12×7＋26＝110万元　　8分
　　第二种方案：盈利总额，当x = 10时有最大值102，
　　即经过10年盈利总额最大，共盈利102 + 8 = 110万元　　　　　　　　　　　　　　　　　　　 10分
　　两种方案获利相同，但方案二所用时间较长，因此采用方案一较为合算．　　　　 12分

21．(1)解：由题意易得M(－1，0)
　　设过点M的直线方程为代入得
　　　　①　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2分
　　再设A(x₁，y₁)，B(x₂，y₂)，则，
　　
　　∴AB的中点坐标为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分
　　那么线段AB的垂直平分线方程为，令得
　　，即，
　　又方程①中，∴，∴x₀＞3　　　　　　　6分

(2)△ABD是正三角形，则需点D到AB的距离等于　　　　　　　　　　　　　　　8分
　　
　　点到AB的距离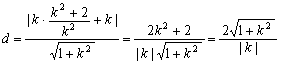　　　　　　　　　　　　　　10分
　　据得：
　　∴，∴，满足
　　∴△ABD可以为正三解形，此时　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

22．(1)解：设直径的两个端点分别为A、B，由椭圆的对称性可得，A、B关于原点O对称，
　　所以A、B点的坐标分别为A(x₁，y₁)，B(－x₁，－y₁)　　　　　　　　　　　　　　　　　　　　　1分
　　P(x，y)是椭圆上任意一点，显然x≠±x₁
　　因为A、B、P三点都在椭圆上，所以有
　　　①
　　　②　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分
　　而
　　①－②：　　　　　　　　　6分
　　所以定理1在椭圆中的推广应为：过椭圆上异于直径两端点的任意一点与一条直径的两个端点连线，则两条连线的斜率之积为定值　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 8分

(2)解：定理1在双曲线中的推广应为：过双曲线上异于直径两端
点的任意一点与一条直径的两个端点连线，则两条连线的斜率之积为定值　　　　　 10分
　　定理1在有心圆锥曲线中的推广应为：过有心圆锥曲线上异于直径两端点的任意一点与一条直径的两个端点连线，则两条连线的斜率之积为定值　　　　　　　　　　　　　　　　　　　　　　　　14分

襄樊市高中调研测试题高二数学(理科)

襄樊市高中调研测试题(2006.1)

高二数学(理科)