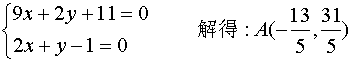![]()
 新疆克拉玛依市2005—2006学年
新疆克拉玛依市2005—2006学年
第一学期高二年级期末考试数学试卷
答卷须知:1.请认真阅读每题的答题要求后,再按要求解题;
2.本卷共19道题,试卷满分为100分,其中一卷1-10题共40分,二卷11-19题共60分;本科目考试时间为100分钟
第一卷
一、选择题(本题共10小题,每题4分,共40分。在每小题给出的四个选项中,只有一个是符合题目要求的,请将正确答案前的字母填入对应的答题栏中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1.给出下列命题:(1) 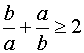 ;(2) 若ac2 < bc2,则a < b;(3)
;(2) 若ac2 < bc2,则a < b;(3) ![]() ;
;
(4) 若a > b,则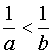 ;(5) 若a>b,c>d ,则a-d > b-c;其中正确的命题有
;(5) 若a>b,c>d ,则a-d > b-c;其中正确的命题有
(A) 1个 (B) 2 个 (C) 3个 (D) 4个
2.若x < 0,则![]() 有
有
(A) 最大值 ![]() (B) 最大值
(B) 最大值 ![]() (C) 最小值
(C) 最小值 ![]() (D) 最小值
(D) 最小值 ![]()
3.直线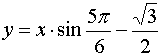 的斜率等于
的斜率等于
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D) ![]()
4.经过两点A(-2,0),B(-5,-3)的直线倾斜角大小为
(A) ![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)
![]()
5.到两坐标轴距离相等的点的轨迹方程是
(A) y=x (B) y = x (C)
y =±x (D) 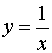
6.若x2 + y 2 + ( m -1 ) x + 2 my + m = 表示圆,则m的取值范围是
(A)
m > 0
(B) m > 1或m < ![]() (C)
(C) 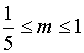 (D) m∈R
(D) m∈R
7. 抛物线 ![]() 的准线方程是
的准线方程是
(A)
![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
8.直线方程为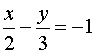 ,则该直线在x、y轴上的截距分别为
,则该直线在x、y轴上的截距分别为
(A) 2,3 (B) 2,-3 (C) -2,-3 (D) -2,3
9.与曲线![]() 共焦点,而与曲线
共焦点,而与曲线![]() 共渐近线的双曲线方程为
共渐近线的双曲线方程为
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
10.圆心在抛物线![]() 上,且与
上,且与![]() 轴和该抛物线的准线都相切的一个圆的方程是
轴和该抛物线的准线都相切的一个圆的方程是
(A) 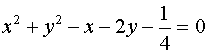 (B)
(B) ![]()
(C) ![]() (D)
(D) 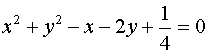
新疆克拉玛依市2005—2006学年
第一学期高二年级期末考试数学试卷
第二卷
二、填空题(本题共4小题,每题3分,共12分,请将答案直接填在题后的横线上)
11.不等式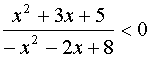 的解集为 ______________________________________
的解集为 ______________________________________
12.直线2x-7y-6=0和x-![]() y+4=0间的距离等于____________________________
y+4=0间的距离等于____________________________
13.若直线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() =___
=___
14.对于椭圆![]() 和双曲线
和双曲线![]() 有下列命题:
有下列命题:
① 椭圆的焦点恰好是双曲线的顶点;
② 双曲线的焦点恰好是椭圆的顶点;
③ 双曲线与椭圆共焦点;
④ 椭圆与双曲线有两个顶点相同.。其中正确命题的序号是 ___________ .
三、
![]()
 解答题(本大题5小题,共48分。解答应写出文字说明,证明过程或演算过程)
解答题(本大题5小题,共48分。解答应写出文字说明,证明过程或演算过程)
15.(8分)已知双曲线方程为5x2-4y2=20,分别求出该双曲线的中心坐标、顶点坐标、焦点坐标、准线方程、渐进线方程、离心率、双曲线上到一个焦点距离为6的点P到两准线的距离。
16.(10分)半径为5的圆过点A(-2, 4),并且以M(-1, 3)为中点的弦长为4![]() ,求此圆的方程.
,求此圆的方程.
17.(10分)已知双曲线![]() 和椭圆
和椭圆![]() :
:![]() 有公共的焦点,它们的离心率分别是
有公共的焦点,它们的离心率分别是![]() 和
和![]() ,且
,且![]() ,求双曲线
,求双曲线![]() 的标准方程.
的标准方程.
18.(10分)已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点(a, -3)到焦点的距离等于5,求a的值,并写出抛物线的方程,准线方程,焦点坐标.
19.(10分)已知ΔABC的两个顶点为B(1,2)和C(-1,-1), ∠A的平分线AD所在直线的方程是2x+y-1=0,求顶点A的坐标.
参考答案:
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | C | B | C | B | A | D | B | D |
二、填空题
11.{x x < - 4或x > 2 } ; 12.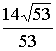 ; 13.±1 ; 14.①、② ;
; 13.±1 ; 14.①、② ;
三、解答题(解答题出现其它解法,阅卷时根据答题情况酌情给分)
15.解:∵5x2-4y2=20 ∴双曲线标准方程为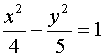
所以中心坐标为(0,0),顶点坐标为(±2,0) ………2分
焦点坐标为(±3,0),
准线方程为x=±![]() ………4分
………4分
渐进线方程为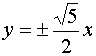 ,离心率e=
,离心率e=![]() ………6分
………6分
P到两准线的距离分别为4和![]() ………8分
………8分
16.解:设所求圆方程为(x-a)2+(y-b)2=25 ………2分
则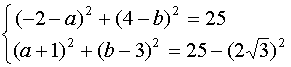 ………6分
………6分
解之可得: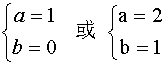 ………8分
………8分
所以所求圆的方程为(x-1)2+y2=25 或(x-2)2+(y-1)2=25 ………10分
17.解:由题易知椭圆C2的焦点坐标为(±5,0),离心率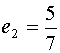 ………2分
………2分
所以可设双曲线C1方程为: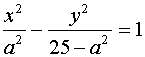 ………5分
………5分
因为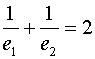 ,所以
,所以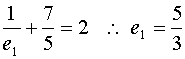 ………7分
………7分
由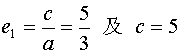 可得a=3
………9分
可得a=3
………9分
所以所求双曲线C1的方程为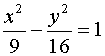 ………10分
………10分
18.解:由题可知抛物线标准方程为x2 =-2py ( p > 0 ) ………2分
由抛物线定义知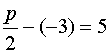 ,解得p=4 ………5分
,解得p=4 ………5分
所以所求抛物线方程为x2 =-8y ………6分
焦点坐标F(0,-2),准线方程为y=2 ………8分
由点(a,-3)在抛物线上,则a2 =-8×(-3)=24 ………9分
所以a=±![]() ………10分
………10分
19. 解1:设A(a,1
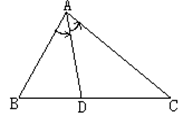
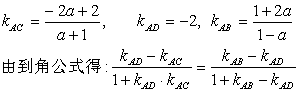
解得:![]() ∴
∴ ![]()
解2:解方程 3x-2y+1=0、2x+y-1=0联立组成的方程组,可得点D(![]() )
)
∵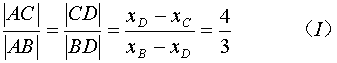
设A(a ,1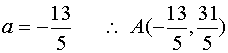
解3:∵∠A的平分线是∠A的对称轴
∴点B(1,2)关于直线AD:2x+y-1=0对称点![]() 在直线AC上,设
在直线AC上,设![]() (x0 , y0)
(x0 , y0)
∵![]()
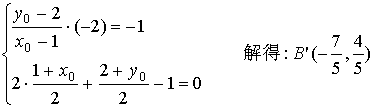
由C(-1,-1)及![]() 解出AC方程:9x+2y+11=0,
解出AC方程:9x+2y+11=0,
由