宜春市2005—2006年度高二年级第一学期期末统考
数 学 试 卷
命题人：李希亮 龚浩生 熊星飞
时间：120分钟 满分：150分
一、选择题：每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内.
1、若
，则
、
、
的大小关系为
（ ）
A、
B、
C、
D、
2、过点
且垂直于向量
的直线方程是
（ ）
A、
B、
C、
D、
3、已知一双曲线的两条渐近线方程为：
及
，则它的离心率是（
）
A、
B、
C、
D、
4、两圆
与
的公共弦所在的直线方程是 （ ）
A、
B、
C、
D、
5、当点
在直线
上移动时 ,
的最小值是 （ ）
A、
B、
C、
D、9
6、以点
为对称中心，直线
关于
对称的直线方程是（
）
A、
B、
C、
D、
7、抛物线
的准线方程是
，则的值为：
（ ）
A、
B、－8
C、
D、8
8 、一动圆与圆
外切，同时与圆
内切，则动圆圆心的轨迹为
（ ）
A、椭圆 B、双曲线的一支 C、抛物线 D、圆
9、已知中心在原点，以坐标轴为对称轴的椭圆，一条弦所在直线方程是
，弦的中点坐标为
，则椭圆的离心率
的值为
（ ）
A、
B、
C、
D、
10、椭圆
上一点
与两焦点
组成一个直角三角形，则点到
轴的距离是
（ ）
A、
B、
C、
D、或
二、填空题(共6小题，每小题4分，共24分．把答案填在题中的横线上)
11、若
，则
的范围是 。
12、直线
与
的夹角是 。
13、过点
圆的
的切线方程是 。
14、过点
和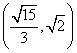
的双曲线标准方程是 。
15、设抛物线
的焦点为F，以
为圆心、
长为半径作一圆与抛物线交于点
、
两点，则
的值是 。
16、直线
与曲线
有两个不同交点，则
的取值范围是____________。
三、解答题(本大题共6小题，满分74分，解答应写出文字说明、证明过程或演算步骤)
17、
解不等式
18、
已知
求
的最大值与最小值。
19、已知圆
内有一点
，
为过点的弦
当弦最短时，求直线的方程；
若
，且直线∥
，求弦的长。
20、某市用37辆汽车往灾区运送一批救灾物资，假设以
的速度直达灾区，已知某市到灾区公路线长
，为安全需要两汽车间距不得小于
。试求这批物资全部到达灾区所用最短时间及车速。
21、设
、
，
、
为直角坐标平面内、轴正方向上的单位向量，若向量
且
求点
的轨迹
的方程
过点
作直线
与曲线交于、
两点，设
。是否存在这样的直线
，使得四边形
是矩形？若存在，求出直线的方程；若不存在，说明理由。
22、直线过定点，且是抛物线
上动弦
的中垂线。
求直线的倾斜角的范围； 求直线与动弦交点的轨迹方程。
宜春市2005——2006年度高二年级第一学期
期末统考数学试卷答案
一、选择题：1、C 2、C 3、C 4、B 5、D
6、D 7、A 8 、A 9、B 10、D
二、填空题：11、
12、
13、
14、
15、8 16、
三、解答题：
17. 解：不等式
①
时
解集为
②当
时
解集为
⑶当
时
解集为
18、解：作出不等式组所表示的平面区域，如图：
其中
，
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
，
则直线
经过A点时，
最小
经过B点时，最大
∴
最小
最大
19、解：⑴当弦AB最短时
∵
，∴
∴直线的方程为：
即：
⑵∵直线∥
∴
，又
直线
∴直线的方程为：
，即
把代入圆的方程
得：
即
设
，
，则
20、设最后一辆车到达时所用时间为
，则
当且仅当
即
时，等号成立
∴
答：这批物资全部到达灾区所用最短时间为
，这时车速为
21、解：⑴ 设
所以点的轨迹是以
为焦点的椭圆，其方程为：
⑵设存在这样的直线 椭圆交于
，
ⅰ.当直线的倾斜角为
时，经检验，不合题意
ⅱ.当直线的斜率存在时，设直线方程为：
与椭圆方程
联立得：
又由题意知：
解得 
存在这样的直线：
，使得四边形是矩形
22.解：解：⑴由题意，斜率存在且不为零，设为，则的方程为，设直线的方程为
由方程组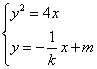
消去得
① ∴
，
∴的中点的坐标为
，
∵在直线上，∴
，即
①中
，即
∴的倾斜角的范围为
⑵设点的坐标为
由⑴得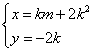
且，∴
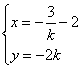消去，得
∵ ∴点的轨迹方程为