英德中学2005~2006年高二数学选修(2-1)期末模拟考试题(答案)
一、选择题(15×4=60分)
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | C | D | C | D | B | A | C | B | D | C |
二、填空题(4×4=16分)
13、![]() (
(![]() ) 14、必要 充分 15、
) 14、必要 充分 15、![]() 16、7
16、7
三、解答题(共74分)
17、(12分)将命题“正偶数不是质数”改写成“若则”的形式,并写出它的逆命题、否命题、逆否命题,并判断它们的真假。
解:原命题:若一个数是正偶数,则这个数不是质数.(假命题)
逆命题:若一个数不是质数,则这个数是正偶数.(假命题)
否命题:若一个数不是正偶数,则这个数是质数.(假命题)
逆否命题:若一个数是质数,则这个数不是正偶数.(假命题)
18、(12分)已知顶点在原点, 焦点在x轴上的抛物线被直线y=2x+1截得的弦长为![]() 。
。
求抛物线的方程.
解:依题意可设抛物线方程为:![]() (a可正可负),与直线y=2x+1截得的弦为AB;
(a可正可负),与直线y=2x+1截得的弦为AB;
则可设A(x1,y1)、B(x2,y2)联立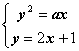 得
得![]()
即:![]()
![]()
![]()
得:a=12或-4
所以抛物线方程为![]() 或
或![]()
19、(12分)已知![]() +
+![]() =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,
求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
解:由![]() ,得F1(2,0),F2(-2,0),F1关于直线l的对称点F1/(6,4),连F1/F2交l于一点,即为所求的点M,∴
,得F1(2,0),F2(-2,0),F1关于直线l的对称点F1/(6,4),连F1/F2交l于一点,即为所求的点M,∴![]() ,∴a=2
,∴a=2![]() ,又c=2,∴b2=16,故所求椭圆方程为
,又c=2,∴b2=16,故所求椭圆方程为![]() .
.
20、(12分)A是△BCD所在平面外一点,M、N分别是△ABC和△ACD的重心.若BD=4,试求MN的长.
![]()
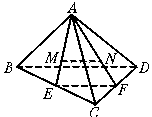
解:连结AM并延长与BC相交于E,又连结AN并延长与CD相交于E,则E、F分别为BC及CD之中点.
现在![]() =
=![]()
=![]() =
=![]() =
=![]() =
=![]()
∴MN=![]() =
=![]()
![]() =
=![]() BD=
BD=![]()
21、(12分)给定双曲线![]() 。过A(2,1)的直线与双曲线交于两点
。过A(2,1)的直线与双曲线交于两点![]() 及
及![]() ,求线段
,求线段![]()
![]() 的中点P的轨迹方程.
的中点P的轨迹方程.
解:设![]() ,
,![]() 代入方程得
代入方程得![]() ,
,![]() .
.
两式相减得: ![]() 。
。
又设中点P(x,y),将![]() ,
,![]() 代入,当
代入,当![]() 时得
时得
![]() 。又
。又![]() , 代入得
, 代入得![]() 。
。
当弦![]() 斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程
斜率不存在时,其中点P(2,0)的坐标也满足上述方程。因此所求轨迹方程
是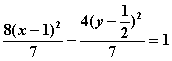 。
。
22、(14分)在棱长为1的正方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 在棱
在棱![]() 上,且
上,且![]() ,H为
,H为![]() 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.
(1)求证:![]() ;
;
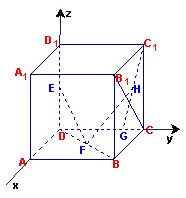 (2)求EF与
(2)求EF与![]() 所成的角的余弦;
所成的角的余弦;
(3)求FH的长.(16分)
解:以D为坐标原点,建立如图所示的空间直角坐标系D-xyz.则![]() ,
,
![]()
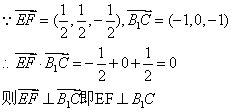
(2)![]() ,由(1)知
,由(1)知
![]()
![]()
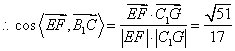
故EF与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(3)![]() 的中点,
的中点,![]()
![]()
四、参考题
23.(05广东卷)(本小题满分14分)
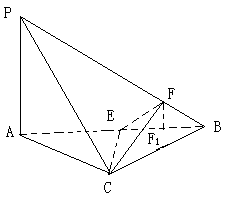 如图3所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=
如图3所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=![]() .F是线段PB上一点,
.F是线段PB上一点,![]() ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B—CE—F的大小.
(I)证明:∵![]()
∴△PAC是以∠PAC为直角的直角三角形,同理可证
△PAB是以∠PAB为直角的直角三角形,△PCB是以∠PCB为直角的直角三角形。
故PA⊥平面ABC
又∵![]()
而![]()
故CF⊥PB,又已知EF⊥PB ∴PB⊥平面CEF
(II)由(I)知PB⊥CE, PA⊥平面ABC
∴AB是PB在平面ABC上的射影,故AB⊥CE
在平面PAB内,过F作FF1垂直AB交AB于F1,则FF1⊥平面ABC,
EF1是EF在平面ABC上的射影,∴EF⊥EC
故∠FEB是二面角B—CE—F的平面角。
![]() 二面角B—CE—F的大小为
二面角B—CE—F的大小为![]()
24、(05广东卷)(本小题满分14分)
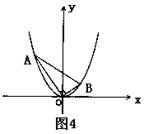
在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图4所示).
(Ⅰ)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)△AOB的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
|
则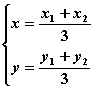 …(1)
…(1)
∵OA⊥OB ∴![]() , 即
, 即![]() ,……(2)
,……(2)
又点A,B在抛物线上,有![]() ,代入(2)化简得
,代入(2)化简得![]()
∴![]()
所以重心为G的轨迹方程为![]()
(II)![]()
由(I)得![]()
当且仅当![]() 即
即![]() 时,等号成立。
时,等号成立。
所以△AOB的面积存在最小值,存在时求最小值1;