高二级选择题训练
姓名 学号 成绩
1、
是复数
为纯虚数的（ ）条件
A、充分非必要 B、必要非充分 C、充分必要 D、既非充分又非必要
2、设
，
，则
在复平面内对应的点位于（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
3、设
是原点，向量
对应的复数分别为
，
，那么向量
对应的复数是（ ）
A、
B、
C、
D、
4、
等于（ ）
A、
B、
C、
D、
5、复数
的值是（ ）
A、
B、
C、
D、
6、如果复数
的实部和虚部互为相反数，那么实数
的值为（ ）
A、
B、
C、
D、
7、已知
，则向量
的夹角为（ ）
A. 
B.
C.
D.
8、下列命题是真命题的是（ ）
A、分别表示空间向量的有向线段所在的直线是异面直线，则这两个向量不是共面向量
B、若
=
，则，的长度相等而方向相同或相反
C、若向量
，
满足＞，且与同向，则＞
D、若两个非零向量与满足＋＝
，则∥
9、空间四边形OABC中，
，点M在OA上，且OM=2MA，N为BC中点，则
等于（ ）
A. 
－＋
B. －＋＋
C. ＋－
D.. ＋－
10、已知向量
的夹角为（ ）
A．0° B．45° C．90° D．180°
11、若
、
、
三个单位向量两两之间夹角为60°，则++
=（ ）
A．6 B．
C．3 D．
12、平行六面体ABCD-A1B
，则x+y+z等于（
）
A.
1
B.
C.
D.
13、若
, 
, 则
=（ ）
A．
4 B．
14、以下七个命题中为真命题的有（ ）个
①三个非零向量、、不能构成空间的一个基底，则、、共面；
②若两个非零向量、与任何一个向量都不能构成空间的一个基底，则、共线；
③若、是两个不共线的向量，而
，则
构成空间的一个基底；
④若与共线，与共线，则与共线；
⑤向量、、共面即它们所在的直线共面；
⑥如果三个不共面的向量、、满足等式：k1＋k2＋k3＝，那么k1＝k2＝k3＝0；
⑦若∥，则存在唯一的实数λ使＝λ.
A.2个 B.3个 C.4个 D.5个
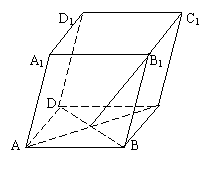15、如图，在平行六面体ABCD–A1B
与BD的交点．若
,
,
,则下列
向量中与
相等的向量是（ ）
A．
B．
C．
D．
16、已知a＝(2，2，1)，b＝(4，5，3)，而n·a＝n·b＝0，且n＝1，则n=（ ）
A．(
，，－)
B．(，－，)
C．(－，，－)
D．±(，－，)
17、A（2，－2），B（4，3），向量p的坐标为（2k－1,－7)且向量p与
平行，则k的值是（ ）
A.
－
B.
C.－
D.
18、复数Z满足条件
，与复数Z对应的点Z的图形是（ ）
A、圆 B、椭圆 C、双曲线 D、抛物线
19、若
则
是
的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
20、已知
（ ）
A．-15 B．
21、平行六面体 
中，E,F,G,H,P,Q是
的中点，则（ ）
A．
B．
C．
D．
22、已知
,当
取最小值时,
的值等于( )
A.19
B.
C. 
D.
23、．已知空间三点O(0，0, 0), A(-1, 1, 0), B(0, 1, 1), 在直线OA上有一点H满足BH⊥OA，则点H的坐标为（ ）
A．(-2, 2, 0) B．(2, -2, 0)
C．
D．
24、在棱长为1的正四面体ABCD中，E, F分别是 BC, AD的中点，则
（ ）
A． 0
B．
C．
D．
25、已知
=（1, 2, 3
） , = ( 3, 0 , – 1),
= (–
, 1, –
), 则在以下结论中：
（1）++=–– ； （2）（++
=2 + 2+ 2；
（3）（•）•=·（·）； （4）（+）·
·（–）,正确的有（ ）.
（A）4个. （B）3个 . （C）2个 . （D）1
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 答案 | B | D | D | D | B | C | C | D | B | C | B | B | D |
| 题号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| 答案 | B | A | D | A | B | A | A | A | C | C | D | A |