首师大附中2005-2006学年度第一学期期末考试
高二数学试题2006.1
班级__________ 姓名 学号_________
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
参考知识:若
,则
,当且仅当
时等号成立.
一、选择题:本大题共8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合
,则
( )
A.
B.
C.
D.
(2)给出平面区域如图所示,目标函数
.若当且仅当
时,目标函数
取得最小值,
则实数
的取值范围是
(
)
A.
B.
C.
D.
(3)设
是双曲线
上一点,双曲线的一条渐近线方程为
分别为双曲线的左、右焦点.若
,则
( )
A.1或7
B
(4)一条铁路原有m个车站,为适应客运的要求需要新增加2个车站,则客运车票增加了26种(注:从甲站到乙站和从乙站到甲站需要两种不同的车票),那么原有车站有 ( )
A.4个 B.5个 C.6个 D.7个
(5)直线
恒过点
( )
A.
B.
C.
D.
(6)关于
的不等式
的解集是
,则实数的取值范围是
( )
A.
B.
C.
D.
(7)直线
与曲线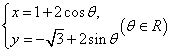
交于A、B两点,则
（
）
A.
B.
C.
D.
(8)已知椭圆
的一条通径(过焦点且垂直于对称轴的弦)与抛物线
的通径重合,则椭圆的离心率为
( )
A.
B.
C.
D.
二、本大题共6小题,每小题4分,共24分.把答案填在题中的横线上。
(9)抛物线
的焦点坐标是____________,准线方程是_____________.
(10)圆
的圆心坐标为__________;若直线
始终平分此圆的周长,则
的取值范围是__________.
(11)过曲线
上任一点M作它的一条渐近线的垂线段,垂足为N,O为坐标原点,则△MON的面积
是___________.
(12)以椭圆
的右焦点为圆心，且与双曲线
的两条渐近线都相切的圆的标准方程
是__________.
(13)已知
是首项为,公比为的等比数列,则
等于___________.(用含
的代数式表示)
(14)直线
过抛物线
的焦点,则直线
截抛物线所得的弦长为___________.
三、解答题:本大题共6小题，共64分.解答应写出文字说明，证明过程或演算步骤。
(15)(本小题满分12分)
(Ⅰ)(6分)已知
,求
的值(用数字作答).
(Ⅱ)(6分)求证:
.
(16)(本小题满分8分)已知抛物线过点
,以
轴为准线,求此抛物线的顶点
的轨迹方程.
(17)(本小题满分12分)已知实轴在轴上的双曲线的渐近线方程为
,且经过点
.
(Ⅰ)试求此双曲线的方程;
(Ⅱ)已知点
,过点引一条直线交双曲线的右支于
两点(
在
的下方),若为弦
的中点，求弦所在的直线方程.
(18)(本小题满分10分)中心在原点
,焦点在轴上的椭圆与直线
相交于
两点,且
,求此椭圆的方程.
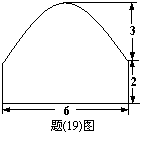(19)(本小题满分10分)如图,一条隧道横截面由一段抛物线及矩形的三边围成,各线段长度见图中所示(单位:米),某卡车空载时可通过此隧道.
(Ⅰ)现有一集装箱,箱宽
条隧道?
(Ⅱ)若卡车载货板离地面
不少于
箱截面积最大?
(20)(本小题满分12分)随
的取值的变化，方程
的直线有无数条，这无数条直线形成了一个直线系,如果直线系中有且仅有一条直线经过点,由所有这样的点组成的集合记为M.
(Ⅰ)试问点
是否是M的元素?为什么?
(Ⅱ)试问:M中的点组成怎样的曲线?
(Ⅲ)设P
,任取
M,
P,如果
的最小值为
,求的值.
参考答案
一. DACC ACAD
二. (9)
(2)
(11)1 (12)
(13)
(14)2006
三.(15)(Ⅰ)1092.(Ⅱ)左
.
(16)
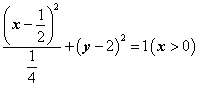
(17) (Ⅰ)
;(Ⅱ)
.
(18)
.
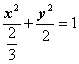(19) (Ⅰ)不能通过;(Ⅱ)长、宽分别为
米、
米时，集装箱截面面积最大.
(20) (Ⅰ)
;(Ⅱ)
,组成的曲线是以
为焦点、直线
为准线的抛物线;(Ⅲ)
.