苏州市2004～2005学年度第二学期高二期终考试
2005.6
数 学
注意事项：
1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共4页．满分150分．考试时间120分钟．
2. 请将第Ⅰ卷的答案填涂在答题卡上，第Ⅱ卷的解答写在答题卷上，在本试卷上答题无效．
第Ⅰ卷（选择题 共60分）
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 球的直径扩大为原来的2倍，则球的体积将变为原来的
(A) 
倍 (B) 
倍 (C) 
倍 (D) 
倍
2. 抛物线
上点
处的切线的倾斜角为
(A) 
(B) 
(C) 
(D) 
3. 直线
互相平行的一个充分条件是
(A) 都平行于同一平面 (B) 与同一平面所成的角相等
(C) 
平行于
所在的平面 (D) 都垂直于同一平面
4. 函数
在区间
上的最大值是
(A) 
(B) 
(C) (D) 
5. 正四面体的侧面与底面所成的二面角的余弦值为
(A) 
(B) 
(C) 
(D) 
6. 
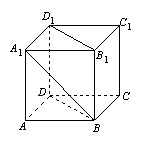如图，在正方体
中，
与平面
所成角的大小为
(A) (B)
(C) (D)
7. 三棱锥
棱锥中，
两两互相垂直，且
，
，则点
到平面
的距离为
(A) 
(B) (C) 
(D) 
8. 长方体的对角线长为
，底面矩形两邻边长分别为
与
，则长方体的体积为
(A) 
(B) 
(C) 
(D) 
9. 若函数
的导函数满足
，则
(A) 
(B) 
为常数函数
(C) 为一次函数 (D) 
为常数函数
10.
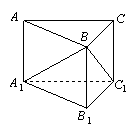如图，直三棱柱
的侧面
是边长为5 的正方形，若
，
与
所成的角为，则长为
(A) 
(B) 
(C) 
(D) 
11.
四面体
中，
，其余棱长均为1，则二面角
的大小为
(A) (B) (C) (D)
12.
已知
在
上是减函数，则的取值范围为
(A) 
(B) 
(C) 
(D) 
第Ⅱ卷（非选择题 共90分）
二．填空题：本大题共4小题，每小题4分，共16分．把答案填在答题卷相应的横线上．
13.
空间向量
与
平行，则
为 ▲ ．
14.
函数
的单调递增区间为 ▲ ．
15.
已知二面角角
的大小为，半平面
内有一条直线
，与棱
所成的角为，则与平面
所成的角为 ▲ ．
16.
在平面几何中有勾股定理：“设
的两边、互相垂直，则
”；拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积和底面积的关系，可以得到的正确结论是：“设三棱锥的三个侧面、
、
两两相互垂直，则 ▲ ”．
三．解答题：本大题共6小题，共74分．请把解答写在答题卷规定的答题框内．解答应写出文字说明、证明过程或演算步骤．
17.
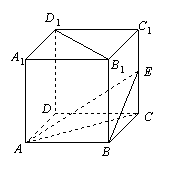(本小题满分12分)
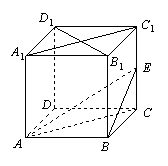
在正方体中，
为棱
的中点．
(Ⅰ) 求证：
；
(Ⅱ) 求二面角
的正切值．
18. (本小题满分12分)
用铁丝制作一个正三棱柱形容器的框架，框架的总长度为
(Ⅰ)把正三棱柱形容器的体积
(m3)表示成底面边长
(m)的函数，并写出相应的定义域；
(Ⅱ)当为何值时，容器的体积最大？求出它的最大值．
19. (本小题满分12分)
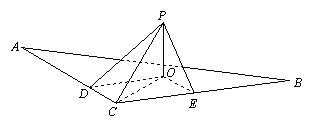
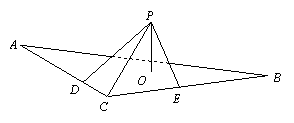在中，
，平面外有一点，
平面，垂足为
．已知
，点到直线
的距离
和
都为
．求：
(Ⅰ) 点到平面的距离；
(Ⅱ) 
与平面所成角的大小．
20. (本小题满分12分)
已知函数
．
(Ⅰ)求
；
(Ⅱ)若
，求
在
上的最大值和最小值；
(Ⅲ) 若在
和
上均单调递增，求的取值范围．
21. (本小题满分12分)
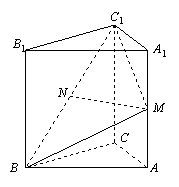如图，在直三棱柱中，
，
，，
是
的中点，
是的中点．
(Ⅰ) 求证：
平面
；
(Ⅱ) 求二面角
的大小．
22. (本小题满分14分)
对于函数
，若同时满足下列两个条件：
①在
上是单调函数；
②存在区间
，使在
上的值域也是．
则称函数为上的闭合函数．
(Ⅰ) 证明函数
为闭合函数，并求出符合条件②的区间；
(Ⅱ) 给出函数
，判断是否为闭合函数，并说明理由；
(Ⅲ) 若
为
上的闭合函数，求实数
的取值范围．
苏州市2004～2005学年度第二学期高二期终考试
数学参考答案和评分标准
说明：
1．本解答仅给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制订相应的评分细则．
2．评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
4．给分或扣分均以1分为单位．选择题和填空题不给中间分．
一．选择题：每小题5分，满分60分．
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | D | C | D | C | A | A | B | B | B | D | D | B |
二．填空题：本题考查基础知识和基本运算．每小题4分，满分16分．
13．2； 14．
； 15．； 16．
．
三．解答题：
17.
本小题满分12分．
解：(Ⅰ)证明：连结
，则
．……………… 2分
又∵
平面
，∴
．
又∵
，∴
平面
．… 4分
又∵
平面，∴．……… 6分
(Ⅱ)解：∵
平面
，
平面，∴
．………………… 8分
又，故
为二面角的平面角． ……………………… 10分
在Rt
中，为的中点，∴
．
因此，二面角的正切值为． ……………………………………… 12分
18. 本小题满分12分．
解：(Ⅰ)∵框架的总长度为
．……………… 2分
∴
．……………………………… 5分
(Ⅱ) 
．………………………………………… 7分
当
时，
，函数
单调递增；
当
时，
，函数单调递减．……………………………… 11分
因此，当
时，容器的体积有最大值为
m3． ………………………… 12分
19. 本小题满分12分．
解：(Ⅰ)连结
，
．
∵平面，且
，∴
．……………………………… 2分
同理
．
∵
，∴
．…………3分
又∵，∴
为正方形．………………4分
∴
，
．……6分
又∵
，
∴
，即点到平面的距离为6．………………8分
(Ⅱ)连结
，则
为与平面所成的角．………………………………9分
∵
，………………………………………………………10分
∴
．
即与平面所成角的为．………………………………………………12分
20. 本小题满分12分．
解：(Ⅰ)由已知，得
．
∴
．……………………………………………………………2分
(Ⅱ)由，得
．
∴
．……………………………………………3分
当
或
时，
；…………………………………………………4分
当
时，
，单调递增；
当
时，
，单调递减；
当
时，，单调递增；……………………………………5分
又
．……………………………… 7分
所以，在上的最大值为
，最小值为
．………………………8分
(Ⅲ)由在和上均单调递增，得在和上
恒成立．
∵的图象是开口向上的抛物线，且经过点
．
∴只要
．………………………………………………………10分
即
解得
．
因此，的取值范围是．……………………………………………………12分
21. 本小题满分12分．
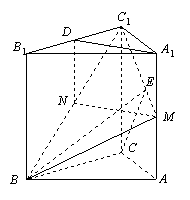解：(Ⅰ)取
的中点，连结
，则
，………………………………1分
且
．
∴四边形
是平行四边形．
∴
．………………………………… 3分
又∵
平面，
平面，
∴平面．………………………… 5分
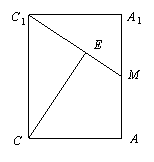(Ⅱ)∵三棱柱是直三棱柱，
∴
．
又∵
，
，
∴
平面
．………………………………7分
在平面内，作
，垂足为，
则由三垂线定理得
，
所以
即为二面角的平面角．……………………………………9分
∵
∽
，∴
．
∴
．…………………………………………… 10分
∴
，∴
．……………………………… 11分
因此，二面角的大小的大小为
．…………………………12分
22. 本小题满分14分．
解：(Ⅰ)∵
，当且仅当
时
，
∴函数在
上单调递减．………………………………………… 2分
设在上的值域为，则
即
，解得
因此，函数为闭合函数，符合条件②的区间为
．…………………4分
(Ⅱ)
，它的值可正可负，………………………… 6分
∴在不是单调函数．
因此，不是闭合函数．…………………………………………………………8分
(Ⅲ)在上，
．
∴
在上是增函数．……………………………………………………10分
∵为上的闭合函数，
∴存在区间
，使在上的值域为．
∴
，即
是方程
的两个 不等正根．…… 12分
∴
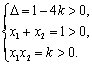解得
．……………………………………………… 14分
因此，实数的取值范围为
．