高二数学期末复习测试题（平面解析几何）
一，选择题
1．下列说法正确的是 （ ）
（A）若直线l1与l2的斜率相等，则l1//l2 （B）若直线l1//l2，则l1与l2的斜率相等
（C）若一条直线的斜率存在，另一条直线的斜率不存在，则它们一定相交
（D）若直线l1与l2的斜率都不存在，则l1//l2
2．若直线
：
不过点
，则方程
表示
（ ）
（A） 与重合的直线 （B）与平行的直线 （C）与相交的直线 （D）可能不表示直线
3,不论m为何实数，直线(m－1)x－y＋2m＋1＝0 恒过定点 （ ）
（A）(1, －
) （B）(－2, 0) （C）(2, 3) （D）(－2, 3)
4,已知
，动点
在线段AB上移动，则
的最大值为 （ ）
(A) 
(B) 
(C) 
(D) 
5,如果直线
沿x轴负方向平移3个单位，再沿y轴正方向平移1个单位后，又回到原来
的位置，则直线的斜率是 （ ）
（A）
（B）3 （C）
（D）－3
6,圆C1: x 2 + y 2 －4x + 6y = 0 与圆C2: x 2 + y 2 －6x = 0 的交点为A、B，则AB的垂直平分线方程为 ( )
A. x + y + 3 = 0 B. 2x －5y －5= 0 C. 3x －y －9 = 0 D. 4x －3y + 7 = 0
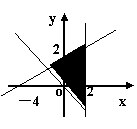
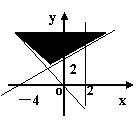
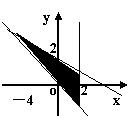
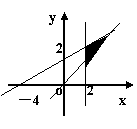7．不等式组
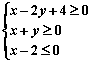表示的平面区域是
( )
8，P是椭圆
+
=1上任意一点，F1、F2是焦点，那么∠F1PF2的最大值是 （ ）
A．600 B．300 C．1200 D．900
9．设Ｆ１、Ｆ２是椭圆
＝１（a＞b＞0）的两个焦点，以Ｆ１为圆心，且过椭圆中心的圆与椭圆的一个交点为Ｍ，若直线Ｆ２Ｍ与圆Ｆ１相切，则该椭圆的离心率是（ ）
A．２－
B．－１ C．
D．
10，焦点为(0，6)且与双曲线
有相同渐近线的方程是（ ）
A. 
B. 
C. 
D. 
11，（2004，天津）设P是双曲线
上一点，双曲线的一条渐近线方程为
、F2分别是双曲线的左、右焦点，若
，则
A. 1或5 B. 6 C. 7 D. 9
12. 如右下图,定圆半径为a，圆心为 ( b ,c ), 则直线ax+by+c=0与直线 x–y+1=0的交点在
A. 第四象限 B. 第三象限 C.第二象限 D. 第一象限
二，填空题
13．直线l：x＋
－1＝0（a∈R）的倾斜角α的取值范围是
14.求与圆A：
=49和圆B：
=1都外切的圆的圆心P的轨迹方程
15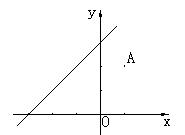
，一条光线经点
处射向
轴上一点B,又从B反射到直线
上的一点C,后又从C点反射回A点,求直线BC的方程
16，（2004，全国）设P为曲线y2=4(x-1)上的一个动点，则点P到点(0,1)的距离与点P到y轴的距离之和的最小值为__________.
三，解答题
17.已知
的两个顶点
，第三个顶点
在直线
上，
求的重心
的轨迹方程.
18．已知圆C：x2+y2-2x+4y-4=0.问是否存在斜率为1的直线l，使l被圆C截得弦AB，以AB为直径的圆经过原点.若存在，写出直线l方程的方程，若不存在，说明理由.
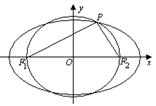
19 (2004全国)设椭圆
的两个焦点是 F1(-c,0),
F2(c,0)(c>0)，且椭圆上存在点P，使得直线 PF1与直线PF2垂直．
(I)求实数 m 的取值范围．
(II)设l是相应于焦点 F2的准线，直线PF2与l相交于点Q. 若
，求直线PF2的方程．
20 (2004，广东)某中心接到其正东、正西、正北方向三个观测点的报告：正西、正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)
21.（2004江苏）已知椭圆的中心在原点，离心率为，一个焦点是F（-m,0）(m是大于0的常数). (Ⅰ)求椭圆的方程； (Ⅱ)设Q是椭圆上的一点，且过点F、Q的直线
与y轴交于点M. 若
，求直线的斜率.
(1)
椭圆为
(2)
设Q（x0,y0）直线：y=k(x+m)则M（0，km）
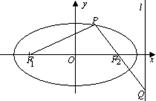
22（2004，天津） 椭圆的中心是原点O，它的短轴长为
，相应于焦点F（c，0）（
）的准线与x轴相交于点A，OF=2FA，过点A的直线与椭圆相交于P、Q两点。
（1）求椭圆的方程及离心率；
（2）若
，求直线PQ的方程；
（3）设
（
），过点P且平行于准线的直线与椭圆相交于另一点M，证明
。
高二数学期末复习测试题（平面解析几何）
一选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | C | C | C | C | D | A | B | B | C | D |
二．填空题
13． [arctan2,
-arctan2] 14.
15．ｙ=-3x+1 16． 
三．解答题
17. 2x-3y+15=0
18．解：设直线L为y-x+b=0以AB为直径的圆为x2+y2-2x+4y-4-
(y-x+b)=0
整理得x2+y2-(2-
x+(4-)y-4-b=0
圆心为（
把圆心代入直线y=x+b得+b=3
有因为x2+y2-(2-x+(4-)y-4-b=0过原点得：b=-4
解之得：b=-1或b=4
直线为y-x+4=0或y-x-1=0
19．解：⑴∵直线PF1⊥直线PF2
∴以O为圆心以c为半径的圆：x2+y2=c2与椭圆：有交点.即
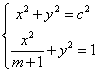有解
又∵c2=a2-b2=m+1-1=m>0
∴
∴
⑵设P(x,y), 直线PF2方程为：y=k(x-c)
∵直线l的方程为：
∴点Q的坐标为(
)
∵ ∴点P分有向线段
所成比为
∵F2(
,0),Q () ∴P(
)
∵点P在椭圆上 ∴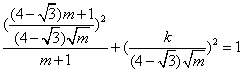
∴
直线PF2的方程为：y=
(x-).
20．解：爆炸点在直线x+y=0和
解之得：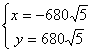
即爆炸点在北偏西680
公里处
21．解:当：
时， F（-m,0）,M(0,km)由定比分点得：x0=-
,y=
Q点在圆上得：
k=
22．解（1）由题意，可设椭圆的方程为
。
由已知得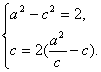
解得
所以椭圆的方程为
，离心率
。
（2）由（1）可得A（3，0）。
设直线PQ的方程为
。由方程组
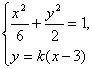
得
依题意
，得
。
设
，则
， ①
。 ②
由直线PQ的方程得
。于是
。 ③
∵，∴
。 ④
由①②③④得
，从而
。
所以直线PQ的方程为
或
（3）证明：
。由已知得方程组
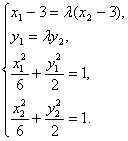
注意，解得
因
，故
。
而
，所以
。