江苏省苏州中学2005～2006学年度第一学期期末考试
高二数学
一、选择题
1.椭圆
上的点
到左准线的距离为
，则点到左焦点的距离为 ( )
A.8
B
D.
2.直线
与双曲线
有且仅有一个公共点，则
的取值为
( )
A.一切实数
B.
或
C.
D.
3.动点在抛物线
移动，则点
与点的连线中点的轨迹方程为 ( )
A.
B.
C.
D.
4.椭圆
(
)的顶点
，
，焦点
，若
，则椭圆的离心率等于
( )
A.
B.
C.
D.
5.圆
：
与圆
：
的交点为
，则
的垂直平分线的方程为
( )
A.
B.
C.
D.
6.与圆
：
相切，且纵截距和横截距相等的直线共有 ( )
A.2条 B.3条 C.4条 D.6条
7.已知抛物线：
与抛物线关于直线
对称，则抛物线的准线方程是 ()
A.
B.
C.
D.
8.设
，则不论取何值，直线
与直线
的交点一定在 ( )
A.一个圆上 B.椭圆上 C.双曲线上 D.抛物线上
9.将4个不同的小球放入编号为1，2，3，4的四个盒子中，恰好有一个空盒的方法数为 ()
A.96
B
10.现有8名同学，从中选出2名男生和1名女生分别参加“资源”、“生态”、“环保”三个夏令营活动，已知共有90种不同的入选方法，那么8名同学中，男生和女生的人数分别为()
A.男生2名，女生6名 B.男生3名，女生5名
C.男生5名，女生3名 D.男生6名，女生2名
二、填空题
11.8个人站成一排，甲、乙两人之间恰有4个人的排法总数为 (结果用数字回答).
12.用1，2，3，4，5这5个数字组成没有重复数字的三位数，共有 个，其中偶数有 个(结果用数字回答).
13.设
是双曲线
的两个焦点，离心率为
，
是双曲线上一点，若
，
，则双曲线的渐近线方程是
，该双曲线方程为 .
14.已知点
在曲线
(
为参数)，则
的最大值为
.
15.把椭圆
绕左焦点按顺时针方向旋转
，则所得椭圆的准线方程为 .
三、解答题
16.“渐升数”是指从左边第二位起每个数字都比前面的数字大的正整数，如125，23478等.
⑴问五位“渐升数”有多少个；
⑵首位为“1”(即1××××)的“渐升数”有多少个；
⑶前两位为“23”(即23×××)的“渐升数”有多少个；
⑷若把五位“渐升数”按从小到大的顺序排列，第100个数为多少？
(以上结果均用数字回答).
17.已知椭圆的中心在原点，焦点在
轴上，为椭圆上一点，
，
，且过点作长轴的垂线恰好过椭圆的一个焦点，求椭圆方程.
18.已知曲线
.
⑴当曲线是椭圆时，求
的取值范围，并写出焦点坐标；
⑵当曲线是双曲线时，求的取值范围，并写出焦点坐标.
19.双曲线
(
)的左焦点
，右焦点
. 过做倾斜角为
的弦
，其中
，当
面积最小值为
时，求
的值.
20.已知点
，点
分别在
轴上滑动，且
，若点
为线段
的中点.
⑴求动点的轨迹的方程；
⑵点
，过点
做直线
交曲线于两点，且
(
)，点
关于轴的对称点为
，已知点
，求证：
；
⑶过点的直线交曲线于
两点，点
关于轴的对称点为
，求证：直线
过定点，并求出定点坐标.
参考答案
一、选择题
1～10. DBCAC CACBB
二、填空题
11.4320.
12.60，24. 13.
，
. 
，
.
三、解答题
16.⑴ 
，五位“渐升数”共126个.
⑵ 
，首位是“1”的五位“渐升数”有70个.
⑶ 
，前两位是“23”的五位“渐升数”有20个.
⑷ ∵前两位是“24”的五位“渐升数”(24×××)有
个，∴若将五位渐升数从小到大排列，第100个数为24789.
17.椭圆方程为().
由条件，知
，
.
又
，∴
.
∴椭圆方程为
.
18.⑴曲线为椭圆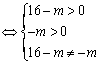
. 即的取值范围是
.
此时，椭圆的焦点在轴上，坐标为
.
⑵曲线为双曲线
. 即的取值范围是
.
此时，双曲线的焦点在轴上，坐标为.
19.
，
.
设直线的方程为：
，其中
.
代入双曲线的方程，并整理得
.
设
，
，则有
，
.
.
∵，∴
.
当
时，
取得最小值
.
由条件，知
，
∵，∴
.
20.⑴设
，则
，
，
，
.
∵ ，∴
.
∴动点的轨迹方程为
.
⑵设
，
，则
.
由，知
，
即
要证明，只要证明
，
即只要证明
由②知④成立. 由①知，要证③，只要证
.
只要证
，只要证
.
∵过点，∴可设直线的方程为
，
代入，并整理得
.
由韦达定理，知
.
∵③，④都成立，∴.
⑶设
，
，则
直线
的方程为 
.
∵过点，∴
，∴
.
∵与关于轴对称，∴
.
∴直线的方程为
，
∵，∴的方程为
，
∴ 直线过定点
.