莆田四中高二数学上学期期末试卷
一、 选择题(每小题5分,共60分)
1. 在下列不等式中,与不等式![]() 同解的是( )
同解的是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
2. 过点![]() ,且圆心在直线
,且圆心在直线![]() 上的圆的方程是( )
上的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.(文)若![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理)设双曲线的半焦距为![]() ,两条准线间的距离为
,两条准线间的距离为![]() ,且
,且![]() ,那么双曲线的离心率等于(
)
,那么双曲线的离心率等于(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 已知两点![]() ,若直线
,若直线![]() 过点
过点![]() ,且与线段
,且与线段![]() 有公共点,则直线
有公共点,则直线![]() 的斜率的取值范围为( )
的斜率的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
5.椭圆![]() 的弦经过点
的弦经过点![]() 且被
且被![]() 平分,则此弦所在直线方程为( )
平分,则此弦所在直线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.(文)过抛物线![]() 的焦点作直线交抛物线于两点
的焦点作直线交抛物线于两点![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理)抛物线![]() 的动弦长为
的动弦长为![]()
![]() ,则动弦
,则动弦![]() 的中点
的中点![]() 到
到![]() 轴的最短距离为( )
轴的最短距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 过点![]() 向圆
向圆![]() 作切线,切线长最小为( )
作切线,切线长最小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. 设![]() 为椭圆
为椭圆![]() 的两焦点,
的两焦点,![]() 在椭圆上,当
在椭圆上,当![]() 的面积为
的面积为![]() 时,
时,![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9. 已知双曲线中心在原点,对称轴在坐标轴上,且过点![]() ,它的一条渐近线的方程为
,它的一条渐近线的方程为![]() ,则双曲线的方程为( )
,则双曲线的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,
,![]() 为空间一定点,则过点
为空间一定点,则过点![]() 且与
且与![]() 所成的角都是
所成的角都是![]() 的直线有( )
的直线有( )
A.3条 B.4条 C.5条 D.6条
11. 在正方体![]() 中,设棱长为
中,设棱长为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,则
的中点,则![]() 与
与![]() 所成的角的余弦值为( )
所成的角的余弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知![]() 和
和![]() 是两个定点,椭圆
是两个定点,椭圆![]() 和等轴双曲线
和等轴双曲线![]() 都以
都以![]() ,
,![]() 为焦点,点
为焦点,点![]() 是
是![]() 和
和![]() 的一个交点,且
的一个交点,且![]() ,对么椭圆
,对么椭圆![]() 的离心率为( )
的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、 填空题(每小题4分,共16分)
13. 对任意实数![]() ,若不等式
,若不等式![]() 恒成立,则的
恒成立,则的![]() 取值范围为
取值范围为![]()
14. 在正方体![]() 中,
中,![]() 和平面
和平面![]() 所成的角为
所成的角为![]()
15. 已知在![]() 中,
中,![]() ,
,![]() ,
,![]() 它所在平面外一点
它所在平面外一点![]() 到
到![]() 三个顶点的距离都是
三个顶点的距离都是![]() ,那么
,那么![]() 到平面
到平面![]() 的距离是
的距离是![]()
16. 下列命题:
①动点![]() 到二定点
到二定点![]() 的距离之比为常数
的距离之比为常数![]() (
(![]() 且
且![]() ),则动点
),则动点![]() 的轨迹是圆;
的轨迹是圆;
②椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,则
,则![]() ;
;
③双曲线![]() 的焦点到渐近线的距离为
的焦点到渐近线的距离为![]() ;
;
④已知抛物线![]() 上两点
上两点![]() ,
,![]() 且
且![]() ,(
,(![]() 为坐标原点),则
为坐标原点),则![]() 的值是
的值是![]() 。
。
以上命题正确的是![]()
莆田四中2004-2005(上)高二数学期末试卷答题卷
一、选择题:(每小题5分,共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二:填空题(每小题4分,共16分)
13![]() 14
14![]() 15
15![]() 16
16![]()
三:解答题(第17—21题,每题12分,22题14分)
17.解关于![]() 的不等式:
的不等式:![]() .
.
18.已知圆![]() 关于
关于![]() 轴对称且经过抛物线
轴对称且经过抛物线![]() 的焦点,若圆
的焦点,若圆![]() 被直线
被直线![]() 分成的两段弧长之比为
分成的两段弧长之比为![]() ,求圆
,求圆![]() 的方程。
的方程。
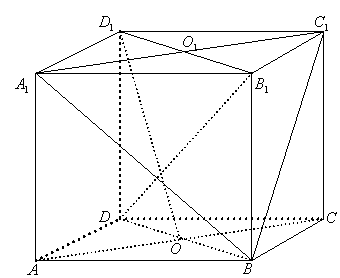 19.如图,已知正方体
19.如图,已知正方体![]() 的棱长为
的棱长为 ![]() ,
,![]() 、
、![]() 分别是正方形
分别是正方形![]() 与正方形
与正方形![]() 的中心。
的中心。
①求证:![]()
![]() ∥平面
∥平面![]()
②求证:![]() 平面
平面![]()
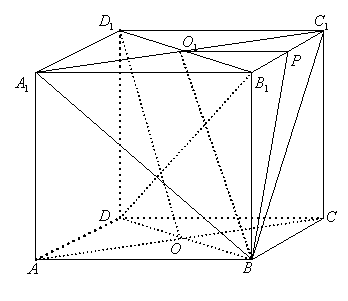
③若![]() 为
为![]() 的中点,
的中点,
求二面角![]() 的正切值。
的正切值。
20.甲、乙两地生产某种产品,它们调出的数量分别为![]() 吨和
吨和![]() 吨。
吨。![]() 三地需要该种产品数量分别为
三地需要该种产品数量分别为![]() 吨,
吨,![]() 吨和
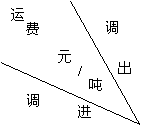
吨和![]() 吨。这些地区调出、调进的数量与运费如下:
吨。这些地区调出、调进的数量与运费如下:
|
| A | B | C | 调出数量 |
| 甲 | 6 | 3 | 5 | 300 |
| 乙 | 5 | 9 | 6 | 750 |
| 调进数量 | 200 | 450 | 400 |
问取怎样的调运方案,才能使总运费最省?
21.已知定点![]() ,
,![]() 动点
动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,并延长
,并延长![]() 到点
到点![]() ,且
,且![]() ,
,![]() 。
。
①求动点![]() 的轨迹方程;
的轨迹方程;
②(文科不做)直线![]() 与动点
与动点![]() 的轨迹交于
的轨迹交于![]() 两点,若
两点,若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围。
的斜率的取值范围。
22.(1)已知![]() 的两个顶点
的两个顶点![]() 、
、![]() ,
,![]() 的内心在直线
的内心在直线![]() 上移动,求第三个顶点
上移动,求第三个顶点![]() 的轨迹
的轨迹![]() 。
。
(2)过![]() 作一条直线交轨迹
作一条直线交轨迹![]() 于
于![]() 两点,问
两点,问![]() 的面积是否有最小值?如果有,求出最小值及这时直线
的面积是否有最小值?如果有,求出最小值及这时直线![]() 的方程;如果没有最小值,请说明理由。
的方程;如果没有最小值,请说明理由。
莆田四中2004-2005(上)高二数学期末试卷答案
一:选择题
1.D 2.C 3.(文)D(理)C 4.B 5.B 6.(文)B(理)D
7.D 8.B 9.A 10.C 11.A 12.A
二:填空题
13.![]() 14.
14.![]() 15.
15.![]() 16.①②③
16.①②③
三:解答题
17.解:原不等式可化为![]()
当![]() 时,原不等式的解集为空集;
时,原不等式的解集为空集;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() 。
。
18.解:抛物线![]() 的焦点为
的焦点为![]() ,
,
设所求圆![]() 的方程为
的方程为![]() , 设
, 设![]() 垂直
垂直![]() 于
于![]()
由题意得![]() ,即
,即![]() , 解得
, 解得![]() ,
,![]()
 所以所求圆
所以所求圆![]() 的方程为
的方程为![]() 。
。
19.证明:
①![]() ∥
∥![]() 且
且![]()
![]() ,
,![]()
![]() ∥
∥![]() 且
且![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]() ∥
∥![]()
又![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
![]()
![]()
![]() ∥平面
∥平面![]()
②![]()
![]() 面
面![]()
![]()
![]() 是线
是线![]() 在面
在面![]() 上的射影
上的射影
![]() ,
,![]() (三垂线定理)
(三垂线定理)
同理![]()
![]()
![]() 平面
平面![]()
③![]() 为
为![]() 的中点又
的中点又![]() 为
为![]() 的中点
的中点 ![]() ∥
∥![]()
![]()
![]()
![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
又![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() ,
,![]()
![]() 就是
就是![]() 的二面角的平面角,
的二面角的平面角,
在![]() 中,
中,![]()
![]() ,
,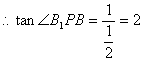
20.解:设由甲地调到A、B两地产品的吨数分别为![]() 和
和![]() ,
,
则由甲地调到C地产品的吨数为![]() ,
,
乙地调到A、B、C三地的数量分别为
![]() ,
,![]() ,
,![]()
且总费用为![]()
![]()
![]() ,
,![]()
由前四式可推得![]()
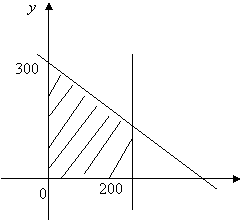 因此约束条件为
因此约束条件为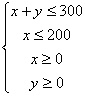 求
求![]() ,
,![]() 的值
的值
下图阴影部分为约束条件,当![]() 时
时
![]() 有最大值为
有最大值为![]() (元)
(元)
![]()
![]()
所以由甲地调到A、B、C地的产品的吨数为![]() ,由乙地调到A、B、C三地的产品的吨数为
,由乙地调到A、B、C三地的产品的吨数为![]() 时,才能使总运费最省。
时,才能使总运费最省。
21.解:(1)设动点![]() 的坐标为
的坐标为![]()
则![]() ,
,
由![]() ,得
,得![]()
因此,动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
(2)设![]() 与抛物线交于点
与抛物线交于点![]()
当![]() 与
与![]() 垂直时,则由
垂直时,则由![]() 得
得![]()
不合题意,故![]() 与
与![]() 轴不垂直;
轴不垂直;
可设直线![]() 的方程为
的方程为![]()
则由![]() ,得
,得![]() ,
,
由点![]() 在抛物线
在抛物线![]() 上,有
上,有![]() ,
,![]()
故![]() ,又
,又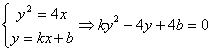
![]() ,
, ![]() ,
,
![]()
![]()
![]()
解得直线![]() 的斜率的取值范围是
的斜率的取值范围是![]() .
.
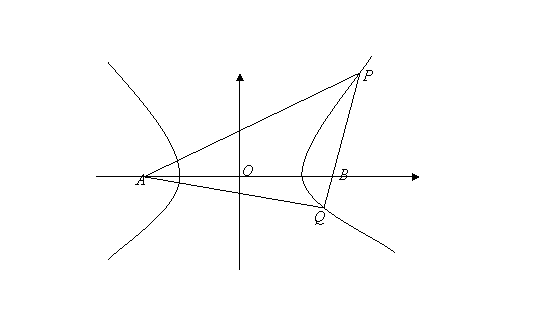
 22.解:(1)如图,设
22.解:(1)如图,设![]() ,过
,过![]() 的内心
的内心![]() 作
作![]() 于
于![]()
![]() 于
于![]() ,
,![]() 于
于![]()
则![]() ,
,![]() ,
,![]()
由![]() 在直线
在直线![]() 上移动得
上移动得![]()
![]() ,
,
![]() ,
,
![]()
故![]() 点在以
点在以![]() 为焦点,实轴长为
为焦点,实轴长为![]() 的双曲线的右支上(去掉右顶点),
的双曲线的右支上(去掉右顶点),
轨迹方程是:![]()
(2)如图,设![]() 的方程为
的方程为![]() ,代入
,代入![]() 点轨迹方程得
点轨迹方程得
![]() ,
,![]()
设![]()
则![]() ,
,![]()
![]()
![]()
![]()
![]()
由于![]() ,故当
,故当![]() 时
时
分子最小,分母最大,![]() 最小
最小
即当![]() 轴时,
轴时,![]() 面积最小,最小值为
面积最小,最小值为![]()

为子