山东省德州一中2005-2006学年
期末综合复习题(理)
命题人：王安拓
2006.1
一．选择题
1.已知椭圆
，则它的离心率与准线方程是（ ）
（A）
（B）
（C）
（D）
2.
（ ）
（A）
（B）－
（C）
（D）－
3.动圆的圆心在抛物线
上，且动圆恒与直线
相切，则动圆必经过定点（ ）
（A）
（B）
（C）
（D）
4.抛物线
到直线
距离最近的点的坐标是（ ）
（A）
（B）
（C）
（D）
5.若
且
，则
的最小值是（ ）
（A）2 （B）3 （C）4 （D）5
6.已知复数
对应的点在第二象限，它的模是3，实部是
，则
是（ ）
（A）
（B）
（C）
（D）
7.正
的边长为
，
是
边上的高，将
沿折起使之与
成
的二面角，这时
点到的距离是（ ）
（A）
（B）
（C）3
（D）
8.设
为椭圆
左、右焦点，过椭圆中心任作一条直线与椭圆交于
两点，当四边形
面积最大时，
的值等于（ ）
（A）0 （B）1 （C）2 （D）4
9.双曲线
两焦点为，点
在双曲线上，直线
的倾斜角之差为
，则
面积为（ ）
（A）
（B）
（C）32
（D）42
10.已知点
，又
是曲线
上的点，则（ ）
（A）
（B）
（C）
（D）
11.设
，集合
，若
为单元素集，则
值得个数为（ ）
（A）1 （B）2 （C）3 （D）4
12.空间四点
每两点的连线都等于
，动点在线段
上，动点
在线段
上，则点与的最小距离是（ ）
（A）
（B）
（C）
（D）
二．填空题
13.已知抛物线
上两点
关于直线
对称，且
，那么
的值为______________________.
14.从双曲线
上任意一点引实轴平行线交两渐近线于
两点，则
之值为______________________.
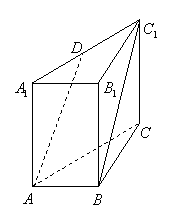
15.如图，在直三棱柱
中，
，
，点
是
的中点，则异面直线
和
所成角的大小为________________.
16.平面
相交于一点
，且两两垂直，点是平面外任意一点且
与平面所成的角是
，则
____________.
三．解答题
17.在复数范围内解方程
（为虚数单位）。
18.设
，是否存在关于
的整式
，使得等式
对大于1的一切自然数都成立？证明你的结论。
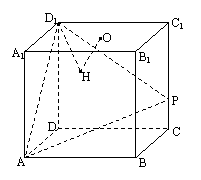
19.在棱长为4的正方体ABCD-A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在棱CC1上，且CC1=4CP.
(1)求直线AP与平面BCC1B1所成的角的大小（结果用反三角函数值表示）；
(2)设O点在平面D1AP上的射影是H，求证：D1H⊥AP；
 |
20.如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），A（
），B（
）
均在抛物线上。
（1）写出该抛物线的方程及其准线方程
（2）当PA与PB的斜率存在且倾斜角互补时，求
的值及直线AB的斜率
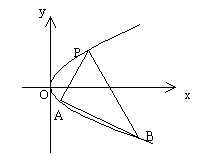
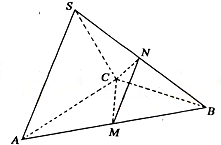
21.在三棱锥S—ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2
，M、N分别为AB、SB的中点.
（1）证明：AC⊥SB；
（2）求二面角N—CM—B的大小；（结果用反三角函数值表示）
（3）求点B到平面CMN的距离.
22.已知椭圆C1的方程为
，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点。
（1）求双曲线C2的方程；
（2）若直线l：
与椭圆C1及双曲线C2恒有两个不同的交点，且l与C2的两个交点A和B满足
(其中O为原点)，求k的取值范围。
期末综合复习题(理)
一．选择题
ABBBB;BACAC;DB
二．填空题
13.
；14. 
；15. 
；16.2。
三．解答题
17. 解：原方程化简为
设
代入上述方程得
解得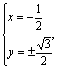
∴原方程的解是
18. 解：假设存在，探索，
当
时，由
，解得
；
当
时，由
，解得
；
当
时，同样可解得
；
由此猜想
。
下面用数学归纳法证明：
当
，
时，等式
成立。
事实上，
（1）当时，
，结论成立；
（2）假设
时结论成立，则
。
这说明
时，等式也成立。
由（1）（2）知，对于大于1的自然数，存在
使
恒成立。
19. 解：（1）解法一：如图所示建立空间直角坐标系
。并由题上的条件知，
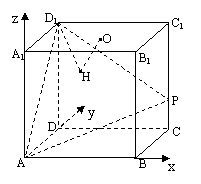A(0,0,0)，B(4,0,0)，P(4,4,1)，
所以
，
可以作为平面BCC1B1的一个法向量，
又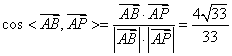
所以，直线AP与平面BCC1B1所成的角的大小为
。
解法二：连结BP.
∵AB⊥平面BCC1B1， ∴AP与平面BCC1B1所成的角就是∠APB,
∵CC1=4CP,CC1=4，∴CP=I.
在Rt△PBC中，∠PCB为直角，BC=4，CP=1，故BP=
.
在Rt△APB中，∠ABP为直角，tan∠APB=
∴∠APB=
（2）解法一：知D1(0,4,4)，O(2,2,4)，所以
,
又知，O点在平面D1AP上的射影是H，所以
所以，
=0
所以，D1H⊥AP。
解法二：O是正方形A1B1C1D1的中心，所以OD1
平面ACC1A1,所以OD1AP.
又O点在平面D1AP上的射影是H，根据三垂线定理，知D1H⊥AP。
20. 解：（1）由已知条件，可设抛物线的方程为
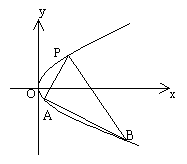
点P（1，2）在抛物线上
，得
故所求抛物线的方程是
准线方程是
（2）设直线PA的斜率为
，直线PB的斜率为
则
，
PA与PB的斜率存在且倾斜角互补
由A（），B（）在抛物线上，得
（1）
（2）
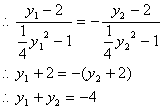
由（1）-（2）得直线AB的斜率
21. 解：（1）取AC中点O，连结OS、OB.
∵SA=SC，BA=BC，
∴AC⊥SO且AC⊥BO.
∵平面SAC⊥平面ABC，平面SAC∩平面ABC=AC
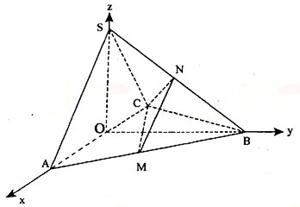∴SO⊥面ABC，∴SO⊥BO.
如图所示建立空间直角坐标系O－xyz.
则A（2，0，0），C（－2，0，0），
S（0，0，2），B（0，2
，0）.
∴
=（－4，0，0），
=（0，－2，2），
∵·=（－4，0，0）·（0，－2，2）=0，
∴AC⊥BS.
（2）由（Ⅰ）得M（1，，0），
，
，
设
=（x，y，z）为平面CMN的一个法向量，
则 
∴可取=(－1，，－1)， 又
=(0，0，2)为平面ABC的一个法向量，
∴cos(，)=
=
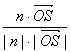∴二面角N－CM－B的大小为arccos
（3）由（Ⅰ）（Ⅱ）得
=（2，2，0），
=（－1，，－1）为平面CMN的一个法向量，
∴点B到平面CMN的距离d=
22. 解：（1）设双曲线C2的方程为
，则
故C2的方程为
（2）将
由直线l与椭圆C1恒有两个不同的交点得
即
①
.
由直线l与双曲线C2恒有两个不同的交点A，B得
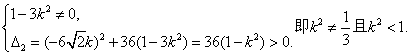
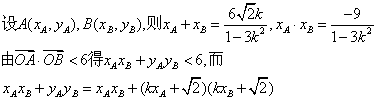
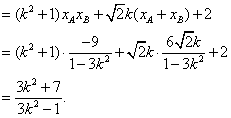
解此不等式得
③
由①、②、③得
故k的取值范围为