弥勒职教中心2005——2006学年下学期期末统测
高 二 数 学 试 题
（考试时间120分钟 全卷满分150分）
参考公式
三角函数的积化和差公式
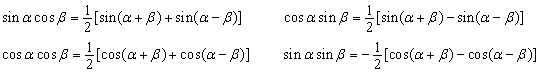
如果事件
、
互斥，那么
如果事件、相互独立，那么
如果事件在一次试验中发生的概率是
，那么
次独立重复试验中恰好发生
次的概率是
球的表面积公式 
其中
表示球的半径
球的体积公式 
其中表示球的半径
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符个题目要求的。
1．已知集合
则集合
（ ）
A．
B．
C．
D．
2．函数
的反函数为（ ）
A．
B．
|
D．
3．已知
为第三象限角，则
是（ ）
A．第一、三、四象限角 B．第一、一、三象限角
C．第一、二、四象限角 D．第二、三、四象限角
4．已知向量
满足：
（ ）
A．
B．
C．
D．
5．（理）将一枚正方体骰子(六个面分别标有点数1、2、3、4、5、6)先后抛掷2次，骰子朝上的面的点数分别为
、
，则
的概率为（ ）
A．
B．
C．
D．
（文）将一枚正方体骰子(六个面分别标有点数1、2、3、4、5、6)先后抛掷2次，骰子朝上的面的点数分别为、，则
的概率为（ ）
A． B． C． D．
6．正四面体的外接球的球面面积为
，与每条棱都相切的球面面积为
，则
（ ）
A．
B．
C．
D．
7．若双曲线
的焦点到它相对应的准线的距离是
，则
（ ）
A．1 B．
8．不等式
的解集为（ ）
A．
B．
C．
D．
9．等差数列
中，
，则此数列前
项的和等于（ ）
A．
B．
C．
D．
10．过点
且平行于直线
的直线方程为（ ）
A．
B．
C．
D．
|
11．下列四个命题中是真命题的为（ ）
A．
B．
C．
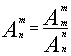D．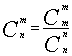
12．
名同学准备参加数学、物理、化学、计算机四项竞赛，每人限参加一项，则不同的参赛方法有（ ）
A．
种 B．
种 C．
种 D．
种
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分
13．设
满足约束条件
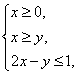
则
的最大值是
14．若
，则
的值为
15．
的展开式中
的系数为
16．在
中，已知
的面积为
，则
的值为
三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。
17．（本小题满分12分）
已知为第二象限角，且
，求
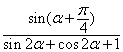的值。
|
18．（本小题满分12分）
已知函数
是定义在
上的减函数，且
。若
。求 （1）
和
的值，
（2）满足
的
的取值范围。
19．（本小题满分12分）
已知数列满足
（1）求
，
（2）求证数列的通项公式为
。
 |
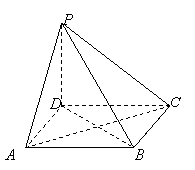20．（本小题满分12分）如图，在四棱锥
中，底面
是
正方形，侧棱
底面，
。
（1）求点
到平面
的距离，
（2）设平面
与平面
所成二面角为
(锐角)，求的大小。
21．（本小题满分12分）
已知倾斜角为
的直线
与抛物线
交于、两点，
，且直线过抛物线的焦点
。
（1）求
的值，
（2）分别过点、作
、
垂直抛物线的准线于
、两点，求证直线
与直线
垂直。
22．（本小题满分14分）
已知函数的解析式为
（1）求的反函数
，
|
，证明数列
是等差数列，并求
。