解析几何直线的位置关系

解析几何直线的位置关系85-3

一、选择题　　　　

1、

已知直线₁：(2a＋5)x＋(a-2)y＋4=0和₂：(2-a)x＋(a＋3)y-1=0互相垂直，则a的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

　　(A)-2　　　　　 (B)2　　　　　 (C)2或-2　　　　  (D)2或-2或-3

翰林汇

2、

四条直线y=3x，y=x-3，x＋y-4=0和x-4y＋11=0的交点个数共有　　( 　 )

　  (A)3　　　　　　  (B)4　　　　　　 (C)5　　　　　　　 (D)6

翰林汇

3、

两条直线x＋y＋5=0与3x＋y-4=0的夹角是　　　　　　　　　　  (　　)

　　(A)arctg　　　　　　　　　　　　(B)

　　(C)arctg()　　　　　　　　　    (D)

翰林汇

4、

若直线₁和₂的斜率是方程6x²＋x-1=0的两根，则₁与₂的夹角等于(　　)

　　(A)60⁰　　 　　　 (B)45⁰　　　　　　  (C)30⁰　　　　　　 (D)15⁰

翰林汇

5、

若直线₁：Bx-2y＋2=0和_2;2x＋6y＋C=0相交于点(1，m)，且₁到₂的角为，则B，C与m的值分别是　　　　　　　　　　　　　　　　　　　 (　　)

　  (A)-1、4、-4　　 (B)-4、-1、4　　 (C)-4、4、-1 　 (D)4、-4、-1

翰林汇

6、

直线y=-2x＋3到y轴所成的角是　　　　　　　　　　　　　　　　 (　　)

　　(A)arctg2　　　　　　　　　　　　 (B)

　　(C)　 　　　　　　　　　(D)

翰林汇

7、

已知直线₁：x＋y=0，₂：kx-y＋1=0，若₁和₂的夹角为60⁰，则k的值为(　　)

　  (A) 或0　　　　 (B)-或0　　　　  (C)　　　　  (D)-

翰林汇

8、

直线₁：x-3=0与直线₂：2x-3y=1的夹角是　　　　　　　　　　　 (　　)

　　(A)-arctg　　(B)-arctg　　(C)arctg　　(D)＋arctg

翰林汇

9、

已知₁：x-3y＋7=0，₂：x＋2y＋4=0，下列说法正确的是　　　　　　　 (　　)

　　(A)₁到₂的角是3p/4　　　　　　　  (B)₁到₂的角是p/4

　　(C)₂到₁的角是3p/4　　   　　　　 (D)₁与₂的夹角是3p/4

翰林汇

10、

直线x＋y-1=0到直线xsin＋ycos-1=0(<<)的角是　 　　　(　　)

　  (A)-　　　　(B)-　　　　(C)-　　　　 (D)

翰林汇

11、

三条直线x+y=2,x-y=0,x+ay=3构成三角形，则a的取范围是　　　　 (　　)

(A)a≠±1　　　 (B)a≠1,a≠2　　　 (C)a≠-1,a≠2　　　 (D)a≠±1,a≠2

翰林汇

12、

方程mx+ny+r=0与方程2mx+2ny+r+1=0表示两条平行（不重合）直线的充要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

(A)mn>0且r≠1　　　　　　　　　　　　　　 (B)mn<0且r≠1

(C)m=n=r=2　　 　　　　　　　　　　　　　　(D)m²+n²≠0且r≠1

翰林汇

13、

若三直线2x＋3y＋8=0，x-y-1=0和x＋ky＋k＋=0相交于一点，则k的值等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

　  (A)-2　　　　　　 (B)-　　　　　　 (C)2　　　　　  (D)

翰林汇

14、

已知两直线3x＋2y-3=0与6x＋my＋1=0互相平行，则它们之间的距离等于(　　)

　  (A)4　　　　　  (B)　　　　 (C)　　　　　 (D)

翰林汇

15、

实数a=0是直线ax-2y=1与2ax-2y=3平行的　　　　　　　　  (　　)

(A)充分不必要条件　　　　　　　　　 (B)必要不充分条件

(C)充要条件　　　　　　　　　　　　 (D)既不充分也不必要条件

翰林汇

16、

方程Ax＋By＋C=0与2Ax＋2By＋C＋1=0表示两条平行直线的条件是 (　　)

　  (A)AB>0且C≠1　　　　　　　　　　  (B)AB<0且C≠1

　　(C)A²＋B²≠0且C≠1　　　　　　　　  (D)A=B=C=1

翰林汇

17、

直线mx＋y－n=0和x＋my＋1=0平行的条件是　　　　　　　　　　  (　　)

　　(A)m=1　　　　　　　　　 (B)m=±1

　　(C)m=1，n¹－1　　　　　　  (D)m=1，n¹－1或m=－1，n¹1

翰林汇

18、

设直线l₁，l₂的倾斜角分别为θ₁和θ₂，下面给出四个命题：

(1)θ₁＝θ₂l₁∥l₂；

(2)θ₁－θ₂＝90⁰l₁⊥l₂；

(3)若l₁，l₂都过原点，且θ₁＋θ₂＝，则l₁和l₂关于y轴对称；

(4)若l₁，l₂都过原点，且θ₁＋θ₂＝0，则l₁和l₂关于x轴对称

其中正确的命题的个数是　　　　　　　　　　　　　　　　　　  (　　)

(A)1　　　　　　  (B)2　　　　　　  (C)3　　　　　　  (D)4

翰林汇

19、

直线(2m²－3m＋1)x＋(m²－m)y=m＋1与直线2x－3y=4平行，那么m的值等于

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

(A)－或1　　　　 (B)－ 　　　　　　(C)或1　　　　　 (D)

翰林汇

20、

直线2x＋y＋m=0与直线x－2y＋n=0的位置关系是　　　　　　　 (　　)

(A)平行　　(B)相交但不垂直　　(C)垂直　　(D)不确定的，与m，n有关

翰林汇

21、

若l₁和l₂的夹角与l₁到l₂的角都等于θ，则cosθ的取值范围是　　　(　　)

(A)[－1，1]　　　　(B)(－1，1)　　　　(C)[0，1]　　　　(D)(0，1)

翰林汇

22、

若两条直线3x＋y＋a=0和x＋y＋b=0平行，则　　　　　　　　 (　　)

(A)a=0，b=0；　　　(B)a＝3，b＝1；　　　(C)a＝3b；　　　(D)a≠3b

翰林汇

23、

直线ax＋(1－a)y=3与直线(a－1)x＋(2a＋3)y=2互相垂直，则a的值为(　　)

(A)－3　　　　  (B)1　　　　　 (C)0或－　　　　　 (D)1或－3

翰林汇

24、

直线2mx＋ny＋1=0与直线nx－2my－1=0的位置关系　　　　　　  (　　)

(A)是垂直　　　　　　　　　　　  (B)是否垂直与m，n的值有关

(C)是平行　　　　　　　　　　　  (D)是相交但不垂直

翰林汇

25、

若集合P={(x，y)y=a(x-1)＋2}，Q={(x，y)y=x}，P∩Q为单元素集，则a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

　　(A)a£-1或a=2　　　　　　　　　　　 (B)a³1，或a=2

　　(C)-1£a£1或a=2　　　　　　　　　　 (D)-1£a<1或a=2

翰林汇

26、

平行直线5x-12y＋26=0与10x-24y-26=0的距离是　　　　　　　　  (　　)

　　(A)6　　　　　　　 (B)5　　  　　　　 (C)4　　　　　　　　 (D)3

翰林汇

27、

两条不重合的直线mx＋y-n=0，x＋my＋1=0互相平行的条件是　　　 (　　)

　　(A)m=1，n=-1　　　　　　　　　 (B)m=n=-1

　　(C)m=1，n¹-1或m=-1，n¹1　　　 (D)m=1，n=1

翰林汇

28、

已知两直线₁：A₁x＋B₁y＋C₁=0 ₂：A₂x＋B₂y＋C₂=0，则₁⊥₂的充分但不必要条件是　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

　　(A)·=-1　 　　　　　　　　　　 (B)=

　　(C)A₁A₂＋B₁B₂=0　 　　　　　　　　　　(D)A₁B₂＋A₂B₁=0

翰林汇

29、

过点P(m，2m＋2)、Q(1，4)的直线与2x-y-3=0平行，则m的值是　 (　　)

　　(A)m¹1　　　　  (B)m=-1　　　　　  (C)m¹-1　　　　　  (D)m=1

翰林汇

30、

与两条平行直线5x-2y-6=0，10x-4y＋2=0等距离的点的轨迹方程是　(　　)

　　(A)20x-8y-9=0　　 　　　　 (B)10x-4y-5=0

　　(C)5x-2y-3=0　　　　　　  (D)15x-6y-11=0

翰林汇

二、填空题　　　　

1、

若直线(m＋2)x-y-3=0与直线(3m-2)x-5y＋1=0互相垂直，则m的值为___。

翰林汇

2、

已知两平行直线分别过点(1，0)和(0，5)，且距离为5，则它们的方程是_____。

翰林汇

3、

已知直线l₁：px+3y+1=0和l₂： 6x+2y－5=0.

(1)如果l₁//l₂, 则p=________;

(2)如果l₁⊥l₂, 则p=________.

翰林汇

4、

直线x-y＋4=0到直线2x＋6y-17=0的角是　　　　　　　　　 。

翰林汇

5、

三条直线4x＋y-4=0，mx＋y=0及2x-3my-4=0，(1)当m=________时，三条直线相交于同一点；(2)当m=________时，三条直线不能构成三角形。

翰林汇

6、

若三条直线x＋y＋1=0，2x-y＋8=0和ax＋3y-5=0共有三个不同的交点，则a的取值范围是________。

翰林汇

7、

若两条直线ax＋2ay＋1=0和(a-1)x-(a＋1)y-1=0互相垂直，则垂足坐标为_____。

翰林汇

8、

已知直线l₁：(a+2)x+(a+3)y=5与l₂：6x+(2a-1)y=5.

(1) 若l₁与l₂重合, 则a=________;

(2)若l₁与l₂互相平行, 则a=________;

(3) 若l₁与l₂互相垂直, 则a=________;

翰林汇

9、

直线x+1=0与x+2y－3=0的夹角等于____________.

翰林汇

10、

已知直线2x－y=0与mx－y=0的夹角为45⁰, 则m=________.

翰林汇

11、

与直线2x－y+4=0的夹角为45⁰, 且与这直线的交点恰好在x轴上的直线方程是____________.

翰林汇

12、

已知直线mx+2y-1=0与直线2x－5y+n=0垂直相交于点(1,a), 则m=________, n=________, a=________;

翰林汇

13、

已知两直线l₁：ax+2y+2=0与l₂：2x+6y+c=0相交于点(1,m), 且l₂到l₁所成的角为45⁰, 则a=________,c=________, m=________.

翰林汇

14、

直线x+my+6=0与直线(m-2)x+3y+m=0相交，则m的范围是_____。

翰林汇

15、

直线x＋2y-1=0到x＋my＋3=0的角是，则m=　　　　　　　　  。

翰林汇

16、

若直线₁：ax＋2y＋8=0，₂：4x＋3y=10，₃：2x-y-10=0相交于一点，则a=____。

翰林汇

17、

若直线l₁和l₂的斜率是方程6x²＋x－1=0的两个根,则l₁与l₂的夹角等于________.

翰林汇

18、

直线x－y=1,x－ky=2,kx－y=3共点,则k=　　　　

翰林汇

19、

已知直线l₁： (m－2)x＋3my＋2m=0和l₂：x＋m²y＋6=0,当m值为_______时, l₁与 l₂相交,当m值为_______时, l₁与 l₂平行; 当m值为_______时, l₁与 l₂重合.

翰林汇

20、

直线₁；x-3y＋1=0与₂：x-3=0的夹角是_________。

翰林汇

三、计算题　　　　

1、

如果直线 l₁：(2m²+m-3)x+(m²-m)y=4m-1与直线l₂：x-3y-5=0互相垂直， 求m的值。

翰林汇

2、

已知直线l₁： ax+by+2a=0 及l₂： (a－1)x+y+b=0 满足下列条件, 分别求a,b的值：

(1)两直线都平行于直线x+2y+3=0;

(2)两直线互相垂直, 且l₁过点(－1,1) .

翰林汇

3、

若a,b,c＞0, 两直线y=xlg(ac)+m和y=xlg(bc)+n互相垂直, 求的取值范围.

翰林汇

4、

已知直线l₁：x+my+6=0,直线l_2：(m-2)x+3y+2m=0, 求m的值, 使得l₁和l₂：　

(1)相交;  (2) 垂直; (3) 平行；  (4) 重合。

翰林汇

5、

已知两直线l₁： (m＋3)x＋2y=5－3m,l₂：4x＋(5＋m)y=16,求分别满足下列条件的m值：(1)l₁与l₂相交;(2) l₁与l₂平行;(3) l₁与l₂重合;(4) l₁与l₂垂直;(5) l₁与l₂夹角为45°.

翰林汇

四、解答题　　　　

1、

设直线l₁：(m+2)x+(1－m)y－3=0与直线l₂：(m－1)x+(2m+3)y+2=0互相垂直,求m的值.

翰林汇

2、

已知直线(2m²+m－3)x+(m²－m)y－4m+1=0与直线x－2y+6=0的夹角为arctg3,求m的值.

翰林汇

3、

已知直线l₁，l₂的方程分别是tx＋2y＋1=0，7x-3ty-5=0，(1)t取何值时，这两条直线相交？(2)t取什么整数值时，这两条直线的交点在第四象限?

翰林汇

4、

直线l过点M(2,3), 且被3x+4y－7=0与3x+4y+8=0截得的线段长为, 求直线l的方程.

解析几何直线的位置关系85-3 〈答卷〉

一、选择题　　　　

1、　C  翰林汇

2、　A  翰林汇

3、　A  翰林汇

4、　B  翰林汇

5、　C  翰林汇

6、　D  翰林汇

7、　A  翰林汇

8、　B  翰林汇

9、　A  翰林汇

10、　D  翰林汇

11、　D  翰林汇

12、　D  翰林汇

13、　B  翰林汇

14、　D  翰林汇

15、　C  翰林汇

16、　C  翰林汇

17、　D  翰林汇

18、　B  翰林汇

19、　D  翰林汇

20、　C  翰林汇

21、　C  翰林汇

22、　D  翰林汇

23、　D  翰林汇

24、　A  翰林汇

25、　D  翰林汇

26、　D  翰林汇

27、　C  翰林汇

28、　A  翰林汇

29、　A  翰林汇

30、　B  翰林汇

二、填空题　　　　

1、　

-或-1

翰林汇

2、　

y=0，y=5或5x-12y-5=0，5x-12y＋60=0

翰林汇

3、　

(1) 9;　 (2) －1.

翰林汇

4、　

p-arctg2

翰林汇

5、　

-1或；-1、、4、-

翰林汇

6、　

a¹-6、a¹3，a¹

翰林汇

7、　

(-)

翰林汇

8、　

(1) 4　 (2) 　(3) －1或

翰林汇

9、　

翰林汇

10、　

或m=－3

翰林汇

11、　

3x+y+6=0或

翰林汇

12、　

m=5,　n=－12 , a=－2.

翰林汇

13、　

a=－1, c=1, .

翰林汇

14、　

m≠3,m≠-1

翰林汇

15、　

翰林汇

16、　

-1

翰林汇

17、　

45°

翰林汇

18、　

4

翰林汇

19、　

m≠0,3,－1;m=0,－1;m=3;

翰林汇

20、　

-arctg

翰林汇

三、计算题　　　　

1、　

解： 由已知， 得1·（2m²+m-3）+(-3)(m²-m)=0, 即m²-4m+3=0， 于是m=1或m=3.　当m=1时，l₁的方程为0=3， 显然不合要求， ∴m=3.

翰林汇

2、　

(1) , b=3;　  (2) a=2, b=－2.

翰林汇

3、　

.

翰林汇

4、　

解：(1) 当m=0时, l₁：x=－6, l₂：2x－3y=0, 显然l₁和l₂相交.

当时, 要l₁与l₂相交, 只需,即m²－2m－30, ∴m3,m-1.

综上知, 当m3且m-1时, l₁与l₂相交;

(2) 要l₁与l₂垂直, 只需(m-2)·1+3m=0, ∴, 即当时，l₁与l₂互相垂直；

（3）要使l₁//l₂，显然m0, 故只需，即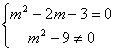

∴m=－1. 即当m=－1时l₁与l₂互相平行；

（4）要使l₁与l₂重合， 由（1）知显然m0， 故只需，即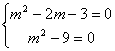， ∴ m=3 即当m=3时，l₁与l₂重合.

翰林汇

5、　

解：由得m²＋8m＋7=0,m₁=－1,m₂=－7,由得m=－1.

(1)当m－1,m－7,,l₁与l₂相交;

(2)m=－7时,,l₁∥l₂;

(3)m=－1时,,l₁与l₂重合;

(4)由A₁A₂＋B₁B₂=0,即4(m＋3)＋2(5＋m)=0,m=－时,l₁l₂;

(5)k₁=－,k₂=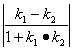－,=tg45°=1,(k₁·k₂－1),k₁,k₂代入化简得

m²＋14m＋29=0,m=－7,

m²＋2m－15=0,m=－5,m=3.

∴当m=－5或3或－7时, l₁与l₂夹角为45°.

翰林汇

四、解答题　　　　

1、　

m=±1

翰林汇

2、　

或－3

翰林汇

3、　

(1)不论t取何实数值，直线₁和₂都相交；(2)t=-1，0，1，2，3.

翰林汇

4、　

x－7y+19=0或7x+y－17=0.

翰林汇

翰林汇