2004年春湖北省部分重点中学期中联考
高二数学试卷
班级![]() 姓名
姓名![]() 分数
分数![]()
一、选择题:(本大题共12小题,每小题5分,共60分)
1、下列说法正确的是( )
A.两两相交的三条直线共面
B.两条异面直线在同一平面上的射影可以是一条直线
C.一条直线上有两点到平面的距离相等,则这条直线和该平面平行
D.不共面的四点中,任何三点不共线
 2、如图,正方体
2、如图,正方体![]() 的棱长为1,则直线
的棱长为1,则直线![]() 和
和![]() 的距离为( )
的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、![]() 、
、![]() 是两条异面直线,所成的角为
是两条异面直线,所成的角为![]() ,直线
,直线![]() 与
与![]() 、
、![]()
所成的角均为![]() ,则这样的直线
,则这样的直线![]() 有( )
有( )
 A.一条 B.两条
C.四条 D.无数多条
A.一条 B.两条
C.四条 D.无数多条
4、在酒泉卫星发射场某试验区,用四根垂直于地面的
立柱支撑着一个平行四边形的太阳能电池板,可测得
其中三根立柱![]() 、
、![]() 、
、![]() 的长度分别为
的长度分别为![]() 、
、
![]() 、
、![]() ,则立柱
,则立柱![]() 的长度是( )
的长度是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
5、设![]() 、
、![]() 表示平面,
表示平面,![]() 表示不在
表示不在![]() 内也不在
内也不在![]() 内的直线,给出下列命题:
内的直线,给出下列命题:
① 若![]() ,
,![]() ∥
∥![]() ,则
,则![]() ② 若
② 若![]() ∥
∥![]() ,
,![]() ,则
,则![]()
③ 若![]() ,
,![]() ,则
,则![]() ∥
∥![]() 其中正确的命题是( )
其中正确的命题是( )
A.①③ B.①② C.②③ D. ①②③
6、![]() 为正三角形,
为正三角形,![]() 是
是![]() 所在平面外一点,且
所在平面外一点,且![]() ,
,![]() 与
与![]() 的面积之比为
的面积之比为![]() ∶
∶![]() ,则二面角
,则二面角![]() 的大小为( )
的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、要在一个体积为V的三棱柱木块![]() 的两端刨去两个三棱锥
的两端刨去两个三棱锥![]() 和
和![]() ,把剩余部分加工成一个魔术道具,则该道具的体积是( )
,把剩余部分加工成一个魔术道具,则该道具的体积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
8、 命题1:长方体中,必存在到各顶点距离相等的点;
命题2:长方体中,必存在到各棱距离相等的点;
命题3:长方体中,必存在到各面距离相等的点.
以上三个命题中正确的有( )
A.![]() 个 B.
个 B.![]() 个
C.
个
C.![]() 个
D.
个
D.![]() 个
个
9、将正方形![]() 沿对角线
沿对角线![]() 折叠成一个四面体
折叠成一个四面体![]() ,当该四面体的体积最大时,直线
,当该四面体的体积最大时,直线![]() 与
与![]() 所成的角为( )
所成的角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、每个面都是三角形的简单多面体,面数与顶点数的比是![]() ∶
∶![]() ,则这个多面体的面数是( )
,则这个多面体的面数是( )
A.五 B.六 C.七 D.八
11、侧棱长为![]() 的正三棱锥
的正三棱锥![]() 的侧面是直角三角形,且四个顶点都在一个球面上,则该球的表面积为( )
的侧面是直角三角形,且四个顶点都在一个球面上,则该球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 12、如图所示,在单位正方体
12、如图所示,在单位正方体![]() 的面对角线
的面对角线![]() 上存在一点
上存在一点![]() 使得
使得![]() 最短,则
最短,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题共4小题,每小题4分,共16分。将答案填在题中横线上。)
13、类比凸![]() 边形的内角和公式,可得
边形的内角和公式,可得![]() 棱柱相邻侧面所成二面角之和为
.
棱柱相邻侧面所成二面角之和为
.
14、在一个![]() 的二面角内,放置一个玻璃球,球与两个半平面分别相切于
的二面角内,放置一个玻璃球,球与两个半平面分别相切于![]() 、
、![]() 两点,已知
两点,已知![]() 、
、![]() 两点的球面距离是
两点的球面距离是![]() ,则玻璃球的直径为
.
,则玻璃球的直径为
.
15、将边长为![]() 的正方形钢板适当剪裁,再焊接成一个密闭的正四棱柱水箱,并要求这个水箱的全面积等于该正方形钢板的面积(要求剪裁的块数尽可能少,不计焊接缝的面积),则该水箱的容积为
.
的正方形钢板适当剪裁,再焊接成一个密闭的正四棱柱水箱,并要求这个水箱的全面积等于该正方形钢板的面积(要求剪裁的块数尽可能少,不计焊接缝的面积),则该水箱的容积为
.
16、判断下列命题的正确性,并把所有正确命题的序号都填在横线上 .
① 若直线![]() ∥直线
∥直线![]() ,
,![]() 平面
平面![]() ,则直线
,则直线![]() ∥平面
∥平面![]()
② 在正方体内任意画一条线段![]() ,则该正方体的一个面上总存在直线与线段
,则该正方体的一个面上总存在直线与线段![]() 垂直
垂直
③ 若平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]()
![]() ,则平面
,则平面![]() ∥平面
∥平面![]()
④ 若直线![]()
![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]()
![]() 直线
直线![]()
选择题答题栏
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
填空题答案:
13、___________________________ 14、___________________________
15、___________________________ 16、___________________________
三、解答题:(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。)
17、(本小题满分12分)
在![]() 中,
中,![]() ,线段
,线段![]()
![]() 平面
平面![]() ,点
,点![]() 在平面
在平面![]() 上的射影为
上的射影为![]() .
.
 求证:
求证:![]() 不可能是
不可能是![]() 的垂心.
的垂心.
18、(本小题满分12分)
如图所示,已知正![]() 的边长为
的边长为![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 上的三等分点,沿
上的三等分点,沿![]() 、
、![]() 把
把![]() 折成三棱锥
折成三棱锥![]() ,使
,使![]() 、
、![]() 两点重合于点
两点重合于点![]() ,
,![]() 是
是![]() 的中点.
的中点.
 (1)求证:平面
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.

班级![]() 姓名
姓名![]()
19、(本小题满分12分)
在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
 (1)求证:
(1)求证:![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
20、(本小题满分12分)
 在长方体
在长方体![]() 中,
中,![]() ,底边
,底边![]() 上有且只有一点
上有且只有一点![]() 使得平面
使得平面![]() 平面
平面![]() .
.
(1)求异面直线![]() 与
与![]() 的距离;
的距离;
(2)求二面角![]() 的大小.
的大小.
21、(本小题满分12分)
已知正四棱锥![]() 的底面边长和侧棱长均为
的底面边长和侧棱长均为![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() .
.
 (1)求证:直线
(1)求证:直线![]() ∥平面
∥平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角;
所成的角;
22、(本小题满分14分)
已知斜三棱柱![]() 的侧面
的侧面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,侧面
,侧面![]()
![]() 底面
底面![]() ,
,![]() ,二面角
,二面角![]() 为30°.
为30°.
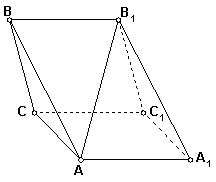 (1)求证:
(1)求证:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(3)在平面![]() 内找一点
内找一点![]() ,使三棱锥
,使三棱锥
![]() 为正三棱锥,并求该棱锥底面
为正三棱锥,并求该棱锥底面![]() 上的高.
上的高.
2004年春湖北省部分重点中学期中联考
高二年级数学试卷参考答案
一、选择题:(每小题5分,共60分)
DCDBA BCBBD DA
二、填空题:(每小题4分,共16分)
13.![]() 14.
14.![]() 15.
15.![]() 16.②④
16.②④
三、解答题:(共74分)
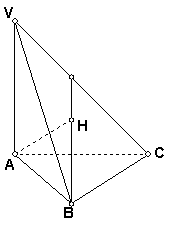 17.(本小题满分12分)
17.(本小题满分12分)
证明:假设![]() 是
是![]() 的垂心…………2分
的垂心…………2分
连结![]() 并延长与
并延长与![]() 相交
相交
∵![]() 平面
平面![]()
∴![]() 是
是![]() 在平面
在平面![]() 内的射影
内的射影
又∵![]()
∴![]() …………………6分
…………………6分
又∵![]() 平面
平面![]()
∴![]() 是
是![]() 在平面
在平面![]() 内的射影
内的射影
∴ ![]() …………………10分
…………………10分
这与![]() 矛盾
矛盾
∴![]() 不可能是
不可能是![]() 的垂心…………12分
的垂心…………12分
 18.(本小题满分12分)
18.(本小题满分12分)
证明:(1)∵![]()
![]()
![]()
∴![]()
![]()
∴![]() 平面
平面![]() …………………3分
…………………3分
又∵![]() 平面
平面![]()
∴平面![]() 平面
平面![]() …………6分
…………6分
(2)在![]() 中,
中,![]()
![]()
![]()
∴![]() ∴
∴![]()
∴![]() …………9分
…………9分
由(1)知![]()
![]() ………12分
………12分
19.(本小题满分12分)
证明:(1)连结![]() ,则
,则![]()
 又∵
又∵![]() ∴
∴![]() 平面
平面![]()
∴ ![]() ………4分
………4分
又∵![]() ∴
∴![]() 平面
平面![]()
∴![]() …………………6分
…………………6分
(2)由(1)知![]() ∵
∵![]()
∵![]()
![]()
∴![]()
![]()
∴![]() …………………8分
…………………8分
设所求距离为![]()
∵![]()
![]()
∴![]()
∴![]() ∴
∴![]() …………12分
…………12分
20.(本小题满分12分)
证明:(1)过![]() 作
作![]() 于
于![]()
∵平面![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]()
 ∴
∴![]() 平面
平面![]()
∴![]()
又∵![]() ∴
∴![]() 平面
平面![]()
∴![]() …………………2分
…………………2分
又∵满足条件的![]() 只有一个
只有一个
∴以![]() 为直径的圆必与
为直径的圆必与![]() 相切,
相切,
切点为![]() ,
,![]() 为的
为的![]() 中点
中点
∴![]() ∴
∴![]() ………4分
………4分
∵![]() 平面
平面![]() ,∴
,∴![]()
又∵![]() ,所以
,所以![]() 为异面直线
为异面直线![]() 与
与![]() 的公垂线段
的公垂线段
![]() 的长度为所求距离
的长度为所求距离 ![]() …………………6分
…………………6分
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,则
,则![]() 平面
平面![]()
过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,则
,则![]()
∴![]() 为二面角
为二面角![]() 的平面角…………………9分
的平面角…………………9分
又∵![]() ,
,![]() 在
在![]() 中
中![]()
 ∴
∴![]() …………………12分
…………………12分
21.(本小题满分12分)
证明:(1)连结![]() 并延长与
并延长与![]() 交于
交于![]()
∵![]() ∽
∽![]()
∴![]()
∴![]()
∴![]() ∥
∥![]() ………………5分
………………5分
又∵![]() 平面
平面![]()
∴![]() ∥平面
∥平面![]() ……………6分
……………6分
(2)∵![]() ∥
∥![]()
∴![]() 、
、![]() 与平面
与平面![]() 所成的角相等…………………8分
所成的角相等…………………8分
设![]() 、
、![]() 交于
交于![]() ,连结
,连结![]() 、
、![]()
∵![]() ,∴
,∴![]() 为所求的角……………9分
为所求的角……………9分
∵![]()
![]() ∴
∴![]()
在![]() 中
中
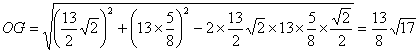 …………10分
…………10分
又∵![]()
![]() ∴
∴![]()
在![]() 中
中 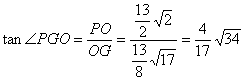
∴![]() …………………12分
…………………12分
22.(本小题满分14分)
 证明:(1)∵平面
证明:(1)∵平面![]() 平面
平面![]()
平面![]() 平面
平面![]()
又∵![]()
![]() 平面
平面![]()
∴![]() 平面
平面![]() …………………4分
…………………4分
(2)取![]() 的中点
的中点![]() ,则
,则![]()
∵![]() 平面
平面![]() ∴
∴![]()
∴![]() 为二面角
为二面角![]() 的平面角 ∴
的平面角 ∴![]()
∵![]() ∴
∴![]() …………………6分
…………………6分
连结![]() ,则
,则![]() 为
为![]() 与平面
与平面![]() 所成的角
所成的角
在![]() 中
中 ![]() …………………9分
…………………9分
(3)在![]() 上取一点
上取一点![]() 使
使![]() ,过
,过![]() 作
作![]() 的平行线与
的平行线与![]() 交于
交于![]() ,则点
,则点![]() 为所求
…………………12分
为所求
…………………12分
∵![]() ∥
∥![]() ∴
∴![]() 平面
平面![]() 且
且![]() 是正
是正![]() 的中心
的中心
∴![]() 为正三棱锥
为正三棱锥
∴所求高为![]() …………………14分
…………………14分