下学期高二期末考试数学（附答案）

湖北省咸宁市2004-2005学年度下学期期末考试

高二数学（A卷）

一、选择题（12×5分）

1．若展开式中存在常数项，则n的值可以是（　）

A．8　　　　　 B．9　　　　　  C．10　　　　　　  D．12

2．集合P={x，1}，Q={y，1，2}，其中x，y∈{1，2，3，4，5，6}，且PQ，把满足上述条件的一对整数（x，y）作为一个点的坐标，则这样的点的个数是（　）

A．7　　　　　 B．8　　　　　  C．9　　　　　　　 D．10

3．m、n表示直线，、、表示平面，给出下列四个命题：

①∩=m，n，n⊥m，则⊥；

②⊥，∩=m，∩=n，则m⊥n；

③⊥，⊥，∩=m，则m⊥；

④m⊥，n⊥，m⊥n，则⊥。

其中正确的命题是（　）

A．①与②　　　B．②与③　　　 C．②与④　　　　　 D．③与④

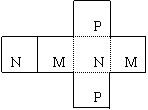
4．如图是一个正方体纸盒的展开图，若把1、2、3、4、5、6分别填入正方形后，按虚线折成正方体，则所得正方体相对面上两个数的和相等的概率是（　）

A．　　　　  B．

C．　　　　 D．

5．已知二面角的平面角为，PA⊥，PB⊥，

A、B为垂足，且PA=4，PB=5，设A、B到二面角的

棱l的距离分别为x、y，当变化时，点（x，y）的轨迹是下列图形中的（　）

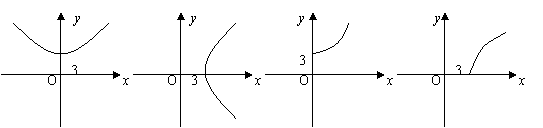A．　　　　　　 B．　　　　　　　 C．　　　　　　　  D．

6．三棱锥V—ABC中，VA=BC，AB=AC，VC=AB，侧面与底面ABC所成的二面角（锐角）分别为、、，则cos+cos+cos的值为（　）

A．　　　　　 B．　　  　　　 C．1　　　　　　  D．2

7．已知～（0，），且P（-2≤≤0）=0.4，则P（>2）等于（　）

A．0.1　　　　  B．0.2　　　　　　 C．0.3　　　　　  D．0.4

8．在如图1×6的矩形　　　　　　　　　　　 中，涂上红、黄、蓝三种颜色，每种颜色取胜余两格，且相邻两格不同色，则不同的余色方法有（　）

A．36 种　　　　B．720种　　　　 C．48种　　　　　 D．30种

9．如果球的表面积为，球面上有A、B、C三点，如果AB=AC=2，BC=，则球心到平面ABC的距离为（　）

A．1　　　　　　 B．　　　　　  C．　　　　　  D．2

10．定义，其中i，n∈N，且i≤n，若

=，则的值为（　）

A．2　　　　　  B．0　　　　　　  C．-1　　　　　　  D．-2

11．在抽查产品的尺寸过程中，将其尺寸分成若干组，[a，b]是其中的一组，所查出的个体在该组上的频率为m，该组上的直方图的高为h，则a-b等于（　）

A．hm　　　　  B．　　　　　　 C．　　　　　　 D．h+m

12．过正方体A₁B₁C₁D₁—ABCD的对角线AC₁的截面是平行四边形AMC₁N，其中M∈A₁B₁，N∈DC，AB=3，BC=1，CC₁=2，当平行四边形AMC₁N的周长最小时，异面直线MC₁与AB所成的角为（　）

A．　　　　 B．　　　　　  C．　　　　　  D．

二、填空题（4×4分）

13．若在二项式的展开式中任取一项，则该项的系数为奇数的概率是　　　 。

第0行　　　　　  1 第1行　　　　　 1　1 第2行　　　　 1　2　 1 第3行　　　 1　3　 3　1 第4行　　 1　4　 6　4  1 第5行　 1　5　10　10　5　1 …　　　　……………

14．如图，在由二项式系数所构成的杨辉三

角形中，第　　　　　 行中从左至右

第14与第15个数的比为2：3。

15．在三棱锥S—ABC中，D是AB的中点，

且SD与BC所成的角为，则二面角

S—AB—C的余弦值为　　　　。

16．如图，正方体A₁B₁C₁D₁—ABCD的棱长

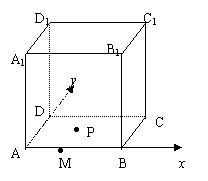为1，点M在A上，且AM=，点P在

平面ABCD上，且动点P到直线A₁D₁的

距离的平方与P到点M的距离的平方差

为1，在XAY直角坐标系中，动点P的

轨迹方程是　　　　　　　　　　 。

三、解答题（5×12+14分）

17．已知袋中有黄色球1个，红色球2个，蓝色球3个，从中任取一球确定颜色且，再放回袋中，取到蓝色球就结束选取，最多可以取3次。

（1）求在三次选取中恰有两次取到红色球的概率；

（2）求取球次数的分布排列。

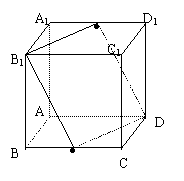18．如图，在棱长为a的正方体ABCD—A₁B₁C₁D₁中，E是BC的中点，平面B₁ED交A₁D₁于F。

（1）指出F在A₁D₁上的位置，并说明理由；

（2）求直线A₁C与DE所成的角的大小。

19．6人到6个地方去旅游，每个人去一个地方，每个地方去一个人。

（1）甲去A地、乙去B地、丙去C地，共有多少种旅游方案？

（2）甲不去A地、乙不去B地、丙不去C地，共有多少种旅游方案？

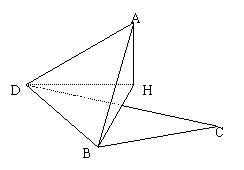20．在平行四边形ABC右，AB=，AD=，，沿BD将其折成二面角A—BD—C，若折后AB⊥CD。

　  （1）求二面角A—BD—C的大小；

（2）求折后点C到面ABD的距离。

21．假设一部机器在一天内发生故障的概率为0.2，机器发生故障时，全天停止工作，若一周的五个工作日里无故障，可获得利润10万元；若发生一次故障可获得利润5万元；发生2次故障获得利润0万元；发生3次或3次以上故障就要亏损2万，求一周的期望利润是多少？

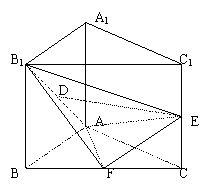22．已知直三棱柱ABC—A1B1C1中，ΔABC为等腰直角三角形，∠BAC=，且AB=AA1，D、E、F分别为B1A、C1C、BC的中点。

（1）求证：DE//平面ABC；

（2）求证：B1F⊥平面AEF；

（3）求二面角B1—AE—F的大小

（用反三角函数表示）

参考答案

1．D　2．B　3．D　4．B　5．D　6．C　7．A　8．D　9．A　10．D　11．B　12．C

13．　　14．34　　15．　　16．

17．解：（1）三次中恰有两次取到红色球的取法有四种情形：红红蓝、红黄红、红红黄、黄红红，故所求概率为。（5分）

（2），，，

∴取球次数的分布列为

	1	2	3
P

18．解：（1）由正方体裁性质，B₁F//ED，B₁E//FD，从而四边形DEB₁F为平行四边形。

∴B₁E=FD，又BB₁=DD₁，故RtΔB₁BE≌RtΔDD₁，

∴D₁F=BE=a，∴F为A₁D₁的中点。（6分）

（2）延长AD至G，使DG=a，连A₁G，则CG//DE。

∠A₁GC为直线A₁1C与DE所成的角。（8分）

，

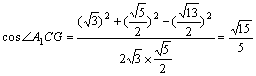∴。（12分）

19．解：（1）=6种方案（5分）

（2）6个人赴6个地方共有种可能。

①若甲、乙、丙同时都去各自不能去的地方旅游，而其余的人去余下的地方旅游的有=6种；

②若甲、乙、丙中有2人同时去各自不能去的地方旅游有种，而3人中剩1人，是种，无条件3人的旅游方法是种，所以共有=54种。（9分）

③若甲、乙、丙中有1人去自己不能去的地方有种，而余下的5人共有种，有2人去自己不能去的地方和1人去自己不能去的地方，共有（--）种。

故满足条件的方案有-（6+54+234）=426（种）。（12分）

20．解：（1）设A点在面BCD上的射影为H，连BH交CD于E，连DG。

在ΔADB中，AD⊥DB，又AH⊥面DBC，∴BD⊥DH。

∴∠ADH为二面角A—BD—C的平面角》（4分）

∵AB⊥CD，AH⊥面DBC，∴BH⊥CD。

易求得，

∵RtΔDEH∽RtΔCEB，∴。

在RtΔADH中，，∴∠ADH=。

∴二面角A—BD—C的大小为。（8分）

（2）由对称性知，C到面ABD的距离等于A到面BCD的距离。

。（12分）

21．解：设随机变量表示一周5天内发生故障的次数。则～（5，0.2），

从而（k=0，1，2，3，4，5）。

∴，，

，

，（7分）

用表示所获得的利润，则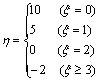

因此一周的期望利润是

E=10×0.328+5×0.410+0×0.205+（-2）×0.057=5.126（万元）（12分）

22．解：（1）连A₁B，必过点D。

连A₁E，并延长A₁E交AC的延长线于P，连BP。

由E为C₁C的中点，A₁C₁//CP可知A₁E=EP。

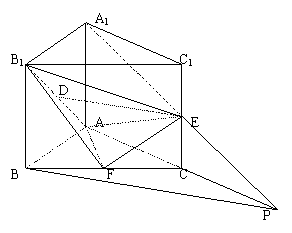∵D₁、E分别是A₁B、A₁P的中点，

∴DE//BP。

又∵BP平面ABC，DE平面ABC，

∴DE//平面ABC。（4分）

（2）∵ΔABC为等腰直角三角形，

∴由三垂线定理得BF⊥AF。

设AB=A₁A=a，则

，，

，

∴+=，∴B₁F⊥EF。

∵AF∩EF=F，∴B₁F⊥平面AEF。

（3）过F作FM⊥AE于点M，连B₁M，

∵B₁F⊥平面AEF，∴B₁M⊥AE（三垂线定理）。

∴∠B₁MF为二面角B₁—AE—F的平面角。

∵C₁C⊥平面ABC，AF⊥FC，∴EF⊥AF（三垂线定理）。

在RtΔAEF中，可求得，

在RtΔB₁FM中，∠B₁MF=，∴，

∴二面角B₁—AE—F的大小为arctan。（14分）