江苏东海县2005年第一学期上学期数学期中考试
高二数学试题
（时间：120分钟 满分：150分）命题人： 冯仰松
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一、选择题：（本大题每小题5分，共60分．在每小题给出的四个选项中,只有一项是符合要求的）
1．已知
，则下列各式中不成立的是 （ ）
A．
B．
C．
D．
2．函数
的定义域是 （ ）
A．（1，＋∞） B．（－∞，2） C．
D．
3．已知定点
在直线
外，则方程
表示 （ ）
A．与
重合的直线 B．与平行的直线 C．与垂直的直线 D．点
4．已知点（2，－1）和（－3,2）在直线
的异侧，则
的取值范围是 （ ）
A．（4,7） B．（－4,7） C．（－7,4） D．（－4,4）
5．不等式
的解集是 （ ）
A．（－∞，2） B．（2，＋∞） C．（－2,2） D．（－∞，－2）∪（2，＋∞）
6．若点A（4，a）到直线4x－3y－1＝0的距离不大于3，则 （ ）
A．－1＜a＜9 B．0≤a≤10 C．5＜a＜8 D．－2≤a≤6
7．若点M（－1，－1）为圆
的弦AB的中点，则直线AB方程是（ ）
A．
B．
C．
D．
8．已知
，则不等式
的解集是 （ ）
A．[－1,2] B．［0,2］ C．［2，＋∞） D．（－∞，2］
9．过点
作圆
的切线，则切线方程为 （ ）
A．
B．
C．
D．
10．由动点P向圆
引两条切线PA、PB，切点分别为A、B，∠APB＝60°，则动点P的轨迹方程是 （ ）
A．
B．
C．
D．
11．过点P（－1，1）作直线l与圆
相交于A、B两点，则｜PA｜·｜PB｜等于 （ ）
A．18 B．19 C．20 D．21
12．直线
到直线
的角为 （ ）
A．
B．
C．
D．
二、填空题：（本大题每小题4分，共16分．把答案填在题中横线上）
13．不等式
的解集是 ．
14．两条直线
与
的交点在第一象限，则的范围是 ．
15．过A（1,2）、B（3,0）两点且圆心在直线y=3上的圆的方程是 ．
16．已知
，且
，则
的最小值为 ．
三、解答题：（本大题共74分）
17．（本题满分12分）通过点P（1,1）作直线l与两坐标轴所围成的三角形面积等于
，求直线l的方程．
18．（本题满分12分）设
，实数满足
．
求证：
．
19．（本题满分12分）求经过点P（1，－1），和直线x－y＝0相切，且圆心在曲线
上的圆的方程．
.
20．（本题满分12分）解关于
的不等式
．
21．（本题满分12分）某工厂生产甲、乙两种产品，已知甲种产品1t需耗A种原料3t、B种原料2t、C种原料1t；生产乙种产品1t需耗A种原料2t、B种原料3t、C种原料2t．工厂在生产这两种产品的计划中要求消耗A种原料不超过190t、B种原料不超过160t、C种原料不超过100t．每1t甲种产品的利润是400元，每1t乙种产品的利润是500元．甲、乙两种产品应各生产多少，能使利润总额最大？
22．（本题满分14分）设M是圆
上动点，O是原点，N是射线OM上点，若｜OM｜·｜ON｜＝120，求N点的轨迹方程．
高二数学试题评分标准
一、选择题：ACBB CBCD ACDD
二、填空题：13．（－∞，－1）∪（－1,0） 14．（－2,1）
15．
16．
三、解答题：
17．设直线的方程为
， ．．．．．．．．1分
直线与x轴、y轴分别相交于A、B
令y=0得A
，令x=0得B
．．．．．．．．3分
△AOB的面积＝
．．．．．．．．6分
∵
无解 ．．．．．．．．8分
由
解得
或
．．．．．．．．10分
∴直线的方程为
或
即
或
．．．．．．．．．12分
18．
＝
．．．4分
∵
∴
．．．6分
又
．．．11分
∴．
19．因圆心在曲线
上，
所以可设圆心坐标为
． ．．．2分
据题意，
，
所以
， ．．．7分
解这个方程，得
或
（舍去）． ．．．10分
所以圆心为（0，－2），半径为
，从而所求圆的方程为
．．．12分
20．原不等式可化为
，于是 ．．．2分
当时，原不等式的解集为（1，＋∞）； ．．．3分
当
时，原不等式可化为
∴当
时，原不等式的解集为
．．．5分
当
时，原不等式的解集为
．．．7分
当
时，原不等式的解集为
．．．9分
当
时，原不等式可化为
，
∴原不等式的解集为
．．．12分
21．设生产甲、乙两种产品分别为xt、yt，利润总额为z元，则
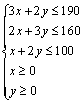．．．4分
．．．5分
作出以上不等式组所表示的平面区域（如图），即可行域 ．．．8分
作直线：
，即直线
，所以直线向右上方平移至
位置时，直线经过可行域上的点M，且与原点距离最大，此时取最大值．
解方程组
得M的坐标为（50,20）． ．．．11分
答：应生产甲产品50t、乙产品为20t，能使利润总额达到最大． ．．．12分
22．设M、N的坐标分别为
、
，
由题设
，得
（＊） ．．．2分
当M不在y轴上时，
，
，于是有
．．．4分
设＝
，代入（＊），化简得 
因
与同号，于是
，
．．．8分
代入并化简，可得
．．．12分
当
时，
，点N
也在直线
上
所以，点N的轨迹方程为． ．．．14分
注：以上评分标准每题仅提供一种解法，如有其它解法可酌情给分．