高二期末总复习练习题（一）
一、 选择题
1、 对任意实数a，b，c给出下列命题：
①“a=b”是“ac=bc”的充要条件 ②“a+5是无理数”是“a是无理数”的充要条件
③“a>b”是“a2>b
其中真命题的个数是（ ）
A、 1 B、
2、
不等式组
的解集是（ ）
A、
B、 
C、
D、 
3、
则a的取值范围是（ ）
A、
B、 
C、
D、 
4、
若x，y是正数，则
的最小值是（ ）
A、3 B、 
C、4 D、 
5、
条件甲：
条件乙：
那么甲是乙的（ ）
A、充分部必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要
6、
将直线
沿x轴向左平移1个单位，所得直线与圆
相切，则实数
的值为（ ）
A、-3或7 B、-2或
7、 从原点向原作两条切线，则该圆夹在两条切线间的劣弧长为：
A、
B、 
C、
D、 
8、设
则
的最小值为（ ）
A、
B、 
C、
D、 
9、过抛物线
的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于5，则这样的直线（ ）
A、有且仅有一条 B、有且仅有两条 C、有无穷多条 D、不存在
10、双曲线
的离心率为2，有一个焦点与抛物线的焦点重合，则
的值为（ ）
A、
B、 
C、
D、 
二、填空题：
11、已知直线
与圆
相交于A、B两点且AB=
，则
12、设实数x、y满足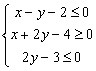
，则z=x+2y的最小值为_____,
的最大值为_____
13、若双曲线的渐近线方程为
，它的一个焦点为
，则双曲线方程为____
14、点p(-3,1)在椭圆
的左准线上，过点p且方向为
的直线，经直线y=-2反射后通过椭圆的左焦点，则这个椭圆的离心率为______
15、设双曲线
的右焦点为F，右准线为
，与两条渐近线交于P、Q两点，如果
是直角三角形，则双曲线的离心率e=________
三、解答题
16、已知
，证明对任意的
恒有
17、已知函数
且方程
有两个实根为
（1）求函数的解析式
（2）设k>1解关于x的不等式
18、在平面直角坐标系中，已知矩形ABCD的长AB为2，宽AD为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合（如图）将矩形折叠，使A点落在线段DC上，若折痕所在的直线的斜率为k，求折痕所在直线的方程.
19、已知椭圆的中心在坐标原点，焦点
在x轴上，长轴
的长为4，左准线于x轴交点为M,且
（1）求椭圆的方程
（2）若直线
为
，P为上的动点，使
最大的点记为Q，求点Q的坐标（用m表示）
20、在平面直角坐标系中，抛物线
上异于坐标原点O的两个不同动点A、B满足
（1）求
重心G的轨迹方程
（2）的面积是否存在最小值？若存在，请求出最小值，若不存在请说明理由
21、已知椭圆
的方程为
，双曲线
的左、右焦点分别为的左、右顶点，而的左、右顶点分别是的左、右焦点
（1）求双曲线的方程
（2）若直线
与椭圆及双曲线都恒有两个不同的交点，且与的两个交点A和B满足
，其中O为原点，求k的取值范围.