钱库第二高级中学数学期末考试试卷4
班级： 姓名：
1．已知
，下列命题正确的是 （ ）
A．
B．
C．
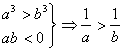D．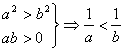
2．过点M（－4，3）和N（－2，1）的直线方程是 （ ）
A．
B．
C．
D．
3．圆
对称的圆的方程是 （ ）
A．
B．
C．
D．
4．过椭圆
的焦点且垂直于x轴的直线l被此椭圆截得的弦长为 （ ）
A．
B．
C．
D．3
5．若
，则与不等式
等价的是 （ ）
A．
B．
C．
D．
6．若a、
成立的充分不必要条件 （ ）
A．
B．
C．
D．
7．与椭圆
共焦点，且两准线间的距离为
的双曲线方程为 （ ）
A．
B．
C．
D．
8．不等式
的最大值是 （ ）
A．
B．
C．
D．
9．两定点A（－2，－1），B（2，－1），动点P在抛物线
上移动，则△PAB重心G的轨迹方程是 （ ）
A．
B．
C．
D．
10．直线
=4得的劣弧所对的圆心角为 （ ）
A．
B．
C．
D．
11．不等式
的解集是 （ ）
A．（－2，0） B．
C．R D．
12．定长为
的线段AB的端点在双曲线
的右支上，则AB中点M的横坐标的最小值为 （ ）
A．
B．
C．
D．
二、填空题
13．若不等式
，则a=
.
14．设椭圆
的右焦点为F1，右准线为l1，若过F1且垂直于x轴的弦长等于F1到l1的距离，则椭圆的离心率为
.
15．F1，F2是双曲线
的两个焦点，P是双曲线上的点，已知PF1，PF2，F1F2依次成等差数列，且公差大于0，则∠F1PF2=
.
16．给出下列命题：
（1）角
的倾斜角
（2）若
的充要条件
（3）若
的最小值为2
（4）若定义
其中正确命题的序号是 .
三、解答题
17．已知不等式
.（1）求a，b的值，
（2）解不等式
（c为常数）.
18．求过点P（1，6）与圆
相切的直线方程.
19．已知椭圆
，其长轴长是短轴长的2倍，右准线方程为
.
（1）求该椭圆方程，
（2）如过点（0，m），且倾斜角为的直线l与椭圆交于A、B两点，当△AOB（O为原点）面积最大时，求m的值.
20．已知抛物线的顶点在原点，它的准线经过曲线
的右焦点，且与x轴垂直，抛物线与此双曲线交于点（
），求抛物线与双曲线的方程.
21．某工厂库存A、B、C三种原料，可用来生产甲、乙两种产品，市场调查显示可获利润等各数据如下表：
| A | B | C | 每件产品利润（元） | ||
| 库存量（件） | 100 | 125 | 156 | （I） | （II） |
| 甲（每件用料） | 1 | 2 | 3 | 2000 | 1000 |
| 乙（每件用料） | 4 | 3 | 1 | 1000 | 3000 |
问：若市场情况如（I），怎样安排生产能获得最大利润?
若市场情况如（II），怎样安排生产才能获得最大利润？
22．已知抛物线
的焦点为F，其准线与x轴交于点M，过点M作斜率为k的直线l交抛物线于A、B两点，弦AB的中点为P，AB的垂直平分线与x轴交于点E（
0）。
（1）求k的取值范围，
（2）求证：
，
（3）△PEF能否成为以EF为底的等腰三角形？若能，求出k的值，若不能，说明理由.
高二（上）数学期末复习题——参考答案
一、1-5 CBBDA 6-10
DABBC 11-12 AD 二、－2 ，
，120°，（4）
三、17．（1）a=1,
b=2
（2）c<－2时，解集为（c,－2）;
c=－2时空集；c>－2时，解集为（－2，c）
18．解：∵圆心为（－2，2） ∴OP=5 则P在圆上，且切线的斜率存在.
设切线方程为
由
19．解（1）
.
又
（2）设
，代入椭圆方程得
令
.
设
又原点O到l的距离
，
，S取得最大值. 即当△AOB的面积最大时，
20．解：由题意可知抛物线的焦点到准线间的距离为2C（即双曲线的焦距）.
设抛物线的方程为
∵抛物线过点
①
又知
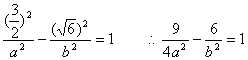②
由①②可得
，∴抛物线为
，双曲线为
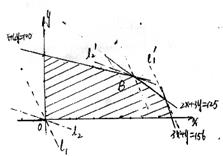21．解：设安排生产产品甲、乙的件数分别为x，y，利润总额为S元.
由题意得约束条件为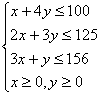
如图，作出可行域.
若市场情况如（I），则目标函数
作直线
. 把l1平移到经过点C时，S取得最大值.
解
，此即所求最优解.
若市场情况如（II）则目标函数
，即
，把l2平移到经过点B时，S取得最大值，
解方程组
，此即所求最优解.
答：若市场情况如（I），应生产甲、乙各49件和9件.
若市场情况如（II），应生产甲、乙各40件和15件.
22．解：由题设有
（1）设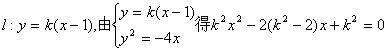
令
（2）设AB中点为
∴AB的垂直平分线的方程为
令
（3）
是以EF为底的等腰三角形.
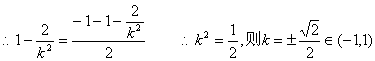
∴△PEF能构成以EF为底的等腰三角形，此时