排列组合二项式定理与概率训练题
一、选择题(本大题共12小题，每小题5分，共60分)
1.3名老师随机从3男3女共6人中各带2名学生进行实验，其中每名老师各带1名男生和1名女生的概率为（ ）
A.
B.
C.
D.
2.某人射击5枪，命中3枪，3枪中恰有2枪连中的概率为（ ）
A. B.
C.
D.
3. 一批产品中，有n件正品和m件次品，对产品逐个进行检测，如果已检测到前k（k＜n
次均为正品，则第k+1次检测的产品仍为正品的概率是（ ）
A.
B.
C.
D.
4. 有一人在打靶中，连续射击2次，事件“至少有1次中靶”的对立事件是（ ）
A.至多有1次中靶 B.2次都中靶 C.2次都不中靶 D.只有1次中靶
5.在一块并排10垄的土地上，选择2垄分别种植A、B两种植物，每种植物种植1垄，为有利于植物生长，则A、B两种植物的间隔不小于6垄的概率为（ ）
A.
B.
C.
D.
6.某机械零件加工由2道工序组成，第一道工序的废品率为a，第二道工序的废品率为b，假定这2道工序出废品是彼此无关的，那么产品的合格率是（ ）
A.ab－a－b+1 B.1－a－b C.1－ab D.1－2ab
7.有n个相同的电子元件并联在电路中，每个电子元件能正常工作的概率为0.5，要使整个线路正常工作的概率不小于0.95，n至少为（ ）
A.3 B
8.一射手对同一目标独立地进行4次射击，已知至少命中一次的概率为
，则此射手的命中率是（ ）
A.
B.
C.
D.
9.
的展开式中的
的系数是（
）
A.275
B
10.有一道竞赛题，甲解出它的概率为
，乙解出它的概率为，丙解出它的概率为，则甲、乙、丙三人独立解答此题，只有1人解出此题的概率是（ ）
A.
B.
C.
D.1
11．事件A与事件B互斥是事件A、事件B对立的（ ）
A.充分不必要条件；B.必要不充分条件；C.充分必要条件；D.既不充分也不必要条件
12．若P（AB）=0，则事件A与事件B的关系是（ ）
A.互斥事件； B.A、B中至少有一个是不可能事件；
C.互斥事件或至少有一个是不可能事件；D.以上都不对
二、填空题（每小题4分，共16分）
13．四封信投入3个不同的信箱，其不同的投信方法有
种
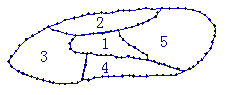14．如图，一个地区分为5个行政区域，
现给地图着色，要求相邻区域不得
使用同一颜色，现有4种颜色可
供选择，则不同的着色方法共有
种
15．若以连续投掷两次骰子分别得到的点数m、n作为点P的坐标，则点P落在直线x+y=5下方的概率是________
16．在编号为1，2，3，…，n的n张奖卷中，采取不放回方式抽奖，若1号为获奖号码，则在第k次（1≤k≤n）抽签时抽到1号奖卷的概率为________
三、解答题（本大题共6小题，共74分解答应写出文字说明、证明过程或演算步骤）
17．（本小题满分12分）设m，n∈Z+，m、n≥1，f（x）=（1+x）m+（1+x）n的展开式中，x的系数为19
（1）求f（x）展开式中x2的系数的最大、小值；
（2）对于使f（x）中x2的系数取最小值时的m、n的值，求x7的系数
18．（本小题满分12分）从5双不同的鞋中任意取出4只，求下列事件的概率：
（1）所取的4只鞋中恰好有2只是成双的；
（2）所取的4只鞋中至少有2只是成双的
19．（本小题满分12分）有8位游客乘坐一辆旅游车随机到3个景点中的一个景点参观，如果某景点无人下车，该车就不停车，求恰好有2次停车的概率
20．（本小题满分12分）已知
的展开式的系数和比
的展开式的系数和大992,求
的展开式中:①二项式系数最大的项;②系数的绝对值最大的项
21．（本小题满分12分）有6个房间安排4个旅游者住宿，每人可以随意进哪一间，而且一个房间也可以住几个人求下列事件的概率：（1）事件A：指定的4个房间中各有1人；（2）事件B：恰有4个房间中各有1人； （3）事件C：指定的某个房间中有两人；（4）事件D：第1号房间有1人，第2号房间有3人
22．（本小题满分14分）已知{
}（
是正整数）是首项是
，公比是
的等比数列
（1） 求和：
；
（2） 由（1）的结果归纳概括出关于正整数的一个结论，并加以证明；
（3） 设
是等比数列的前项的和，求
排列组合二项式定理与概率
参考答案：
1.A 2.B 3.A 4. C 5.C 6.A
7.C 8.B 9.C 10.B 11．B 12．C
13． 
14． 72 15． 
16． 
17．设m，n∈Z+，m、n≥1，f（x）=（1+x）m+（1+x）n的展开式中，x的系数为19
（1）求f（x）展开式中x2的系数的最大、小值；
（2）对于使f（x）中x2的系数取最小值时的m、n的值，求x7的系数
解：
（1）设x2的系数为
T=
∵n∈Z+，n≥1，
∴当
当
（2）对于使f（x）中x2的系数取最小值时的m、n的值，即
从而x7的系数为
18．从5双不同的鞋中任意取出4只，求下列事件的概率：
（1）所取的4只鞋中恰好有2只是成双的；
（2）所取的4只鞋中至少有2只是成双的
解：基本事件总数是
=210
（1）恰有两只成双的取法是
=120
∴所取的4只鞋中恰好有2只是成双的概率为
(2)事件“4只鞋中至少有2只是成双”包含的事件是“恰有2只成双”和“4只恰成两双”，恰有两只成双的取法是
=120，四只恰成两双的取法是
=10
∴所取的4只鞋中至少有2只是成双的概率为
19．有8位游客乘坐一辆旅游车随机到3个景点中的一个景点参观，如果某景点无人下车，该车就不停车，求恰好有2次停车的概率
解：8位游客在3个景点随机下车的基本事件总数有38=6561种
有两个景点停车，且停车点至少有1人下车的事件数有
（
+
+…+
+
）=3（28－1）=381种
∴恰好有2次停车的概率为
20．已知的展开式的系数和比的展开式的系数和大992,求的展开式中:①二项式系数最大的项;②系数的绝对值最大的项
解：由题意
,解得
①
的展开式中第6项的二项式系数最大,
即
②设第
项的系数的绝对值最大,
则
∴
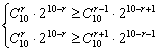,得
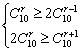,即
∴
,∴
,故系数的绝对值最大的是第4项即
21．有6个房间安排4个旅游者住宿，每人可以随意进哪一间，而且一个房间也可以住几个人求下列事件的概率：（1）事件A：指定的4个房间中各有1人；（2）事件B：恰有4个房间中各有1人； （3）事件C：指定的某个房间中有两人；（4）事件D：第1号房间有1人，第2号房间有3人
解：4个人住进6个房间，所有可能的住房结果总数为：
（种）
（1）指定的4个房间每间1人共有
种不同住法
（2）恰有4个房间每间1人共有
种不同住法
（3）指定的某个房间两个人的不同的住法总数为：
（种），
（4）第一号房间1人，第二号房间3人的不同住法总数为：
（种），
22．已知{}（是正整数）是首项是，公比是的等比数列
⑴求和：；
⑵由（1）的结果归纳概括出关于正整数的一个结论，并加以证明；
⑶设是等比数列的前项的和，求
解：（1）
；
（2）归纳概括出关于正整数的一个结论是：已知{}（是正整数）是首项是，公比是的等比数列，则
证明如下：
=
（3）因为
，所以
=
=-