高中数学系列1-1第三章综合测试题
学校:龙山中学 命题:尉晓峰
一、选择题
1. 曲线y=![]() 在点(
在点(![]() ,
,![]() )处切线的倾斜角为
( )
)处切线的倾斜角为
( )
(A)
![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)![]()
2. ![]() ,则函数
,则函数![]() 可以是下列各式中的哪一个
( )
可以是下列各式中的哪一个
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3. 曲线![]() 在点P处切线的斜率为k,当k=3时P点坐标为
( )
在点P处切线的斜率为k,当k=3时P点坐标为
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4. 下列各式正确的是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5. 方程![]() 的解的个数是
( )
的解的个数是
( )
(A)3 (B)1 (C)0 (D)2
6. 函数![]() 的单调区间是
( )
的单调区间是
( )
(A)增区间为(0,1),减区间为(1,![]() );
);
(B)增区间为(![]() ),减区间为(1,
),减区间为(1,![]() );
);
(C)增区间为(1,![]() ),减区间为(
),减区间为(![]() );
);
|
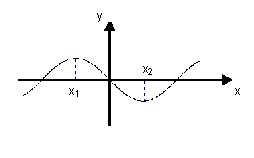
7. 已知函数![]() 的图象如右图所示,
的图象如右图所示,
其中![]() ,
,![]() ,
,
则![]() 值为
( )
值为
( )
(A)![]() ,
,![]() (B)
(B)![]() 1 ,
1 , ![]()
(C)![]() 1.1,
1.1, ![]()
![]() (D)
(D)![]()
![]() ,
,![]()
![]()
8. ![]() 为增函数,则
( )
为增函数,则
( )
(A)![]() (B)
(B)![]()
(C)![]() ,
,![]() (D)
(D)![]()
9. 函数![]() 的最大值是
( )
的最大值是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10. 已知直线![]() 与抛物线
与抛物线![]() :
:![]() ,
,![]() 分别相切于点A、B,且AB
分别相切于点A、B,且AB![]() ,则
,则![]() 的值是
( )
的值是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)1
(D)1
二、填空题
11. 质点运动的方程为![]() ,则质点在
,则质点在![]() 这段时间内的平均速度为
,在
这段时间内的平均速度为
,在![]() 时的瞬时速度为
.
时的瞬时速度为
.
12. 在曲线![]() 的图象上取一点
的图象上取一点![]() 及附近一点(
及附近一点(![]() ),则
),则![]()
![]() __________ ;当
__________ ;当![]() ;过点P的切线方程为
.
;过点P的切线方程为
.
13. 已知函数![]() 在
在![]() 处存在导数
处存在导数![]()
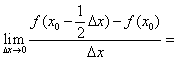 _____.
_____.
14. 圆柱形金属饮料罐的高为![]() ,底面半径为
,底面半径为![]() ,当其表面积一定时,应怎样制作其容积最大,这时
,当其表面积一定时,应怎样制作其容积最大,这时![]() 与
与![]() 的关系是
.
的关系是
.
三、解答题
15. 已知![]() ,
,![]() ,
,![]() ,试求
,试求![]() 的最小值.
的最小值.
16. 已知二次函数![]() 经过点(0,10),导函数
经过点(0,10),导函数![]() 当
当![]()
![]() 时,
时,![]() 的函数值为整数的个数记为
的函数值为整数的个数记为![]() ,求数列{
,求数列{![]() }的通项公式.
}的通项公式.
17. 已知函数![]() (其中
(其中![]() 为自然对数的底数),试讨论函数
为自然对数的底数),试讨论函数![]() 的单调性.
的单调性.
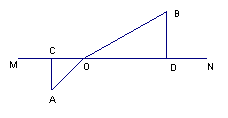
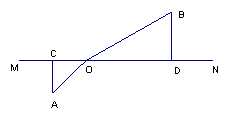
18. 如图所示,直线MN为宽度忽略不计的一条小溪,小溪的一侧是沙地,另一侧是草地,沙地上的点A到小溪MN的距离AC=20Km,草地上的点B到小溪MN的距离BD=30Km,
且CD=70 Km,现有一位骑士要把情报从A送到B,已知骑士在草地上的行进速度是在沙地行进速度的2倍,骑士应选择怎样的行进路线才能尽快将情报送出?
|
高中数学系列1-1第三章综合测试题参考答案
一、选择题
B B C C A D B D A C
二、填空题
11 、 ![]() ,
,![]() ;12、
;12、![]() ,2 ,
,2 ,![]() ;13、
;13、![]() ;14、
;14、![]() .
.
三、解答题
15.解:![]() 设
设![]() 则
则![]()
令![]() ,得
,得![]() 或
或![]() 列表如下:
列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 递增 | 9 | 递减 |
| 递增 |
|
![]() 的最小值为
的最小值为![]()
16.解:![]()
![]() 又
又![]() 经过点(0,10)
经过点(0,10)
![]()
![]()
又![]() 时,
时,![]() 的函数值为整数的个数为
的函数值为整数的个数为![]() ,
,
![]() 在
在![]() 上的值域是
上的值域是![]()
![]()
![]() 在
在![]() 上的值域是
上的值域是![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,
因而![]() 时,
时, ![]() 在
在![]() 上递增,值域为
上递增,值域为![]()
![]()
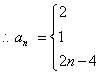
![]()
17.解:因为![]() ,所以
,所以
(1)当![]() 时,令
时,令![]() 得
得![]() ;若
;若![]() ,则
,则![]() ,从而
,从而![]() 在
在![]() 上单调递增;若
上单调递增;若![]() ,则
,则![]() ,
,![]()
(2)当![]() 时,令
时,令![]() 得
得![]() ;若
;若![]() ,则
,则![]() ;从而
;从而![]() 在
在![]() 上单调递减;若
上单调递减;若![]() ,则
,则![]() ,从而
,从而![]() 在
在![]() 上单调递增;若
上单调递增;若![]() ,则
,则![]() ,从而
,从而![]() 在
在![]() 上单调递减.
上单调递减.
|
![]()
![]()
令![]() ,得唯一的极值点
,得唯一的极值点![]() ,
,
∴当O点选在离C点10Km处时,能使骑士从A到B用时最少.