高二数学下学期同步测试（6）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

2004－2005学年度下学期

高中学生学科素质训练

高二数学同步测试（6）— 空间向量

YCY

本试卷分第Ⅰ卷和第Ⅱ卷两部分.共150分.

第Ⅰ卷（选择题，共50分）

一、选择题：（本大题共10个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1．在下列命题中：①若、共线，则、所在的直线平行；②若、所在的直线是异

　 面直线，则、一定不共面；③若、、三向量两两共面，则、、三向量一定

　 也共面；④已知三向量、、，则空间任意一个向量总可以唯一表示为

　 ．其中正确命题的个数为　　　　　　　 　　　　　　　　　　　　　　　　 （　　）

　　　 A．0　　　　　　　　　　B．1　　 　　　　　　　　C．2　　　　 　　　　D．3

2．在平行六面体ABCD－A₁B₁C₁D₁中，向量、、是　　　　　　　　　 （　　）

　　　 A．有相同起点的向量　　　　　　　　　　　　　B．等长向量　　

　　　 C．共面向量　　 　　　　　　　　　　　　　　　　　 D．不共面向量

3．若向量、　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　 B．　

　　　 C．　 　　　　D．以上三种情况都可能

4．已知＝（2，－1，3），＝（－1，4，－2），＝（7，5，λ），若、、三向量共

　 面，则实数λ等于　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　（　　）

A．　　　　　　　　　B．　　　　　　　　　C．　　　　　　　　　 D．

5．直三棱柱ABC—A₁B₁C₁中，若， 则 　　　　　　　　　　 （　　）

　　　 A．+－ 　　　　　B．－+ 　　　　　C．－++　　　　D．－+－

6．已知++＝，＝2，＝3，＝，则向量与之间的夹角为（　　）

　　　 A．30°　　　　　　　　B．45°　　　　　　　C．60°　 　　　　　　　D．以上都不对

7．若、均为非零向量，则是与共线的　　　　　　  　　　　　　　　 （　　）

　　　 A．充分不必要条件　　　　　　　　　　　　　　　 B．必要不充分条件

　　　 C．充分必要条件　　　　　　　　　　　　　　　　　 D．既不充分又不必要条件

8．已知△ABC的三个顶点为A（3，3，2），B（4，－3，7），C（0，5，1），则BC边上的

　 中线长为　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　（　　）

A．2　　　　　　　　　B．3　　　　　　　　　C．4　　　　　　　　　　 D．5

9．已知　　　　　　　　　（　　）

A．－15　　　　　　　　　 B．－5　　　　　　　　　　 C．－3　　　　　　　　　　 D．－1

10．已知，，，点Q在直线OP上运动，则当

取得最小值时，点Q的坐标为　　　　　　　　　　　　　　　 　　　　　　　　　　　（　　）

A．　 　　　 B．　 　　　 C．　　　　　D．

第Ⅱ卷（非选择题，共100分）

二、填空题（本大题共4小题，每小题6分，共24分）

11．若A(m＋1，n－1,3)，B(2m,n,m－2n)，C(m＋3,n－3,9)三点共线，则m+n= 　　　　　　 ．

12．已知S是△ABC所在平面外一点，D是SC的中点，

若＝，则x＋y＋z＝　　　　　　 ．

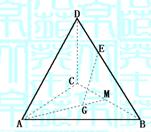
13．在空间四边形ABCD中，AC和BD为对角线，

　　　 G为△ABC的重心，E是BD上一点，BE＝3ED，

　　　 以｛，，｝为基底，则＝　　　　　　  ．

14．设＝1，＝2，2＋与－3垂直，＝4－，

＝7＋2，　则<,>＝　　　　  ．

三、解答题（本大题满分76分）

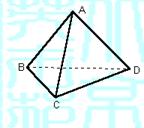
15．(12分) 如图，一空间四边形ABCD的对边

AB与CD，AD与BC都互相垂直，

用向量证明：AC与BD也互相垂直．

16．（12分））如图，在棱长为2的正方体ABCD－A₁B₁C₁D₁中，

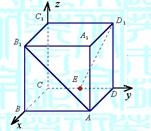
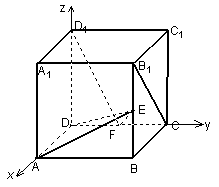
　　　 E是DC的中点，取如图所示的空间直角坐标系．

　 （1）写出A、B₁、E、D₁的坐标；

　 （2）求AB₁与D₁E所成的角的余弦值．　

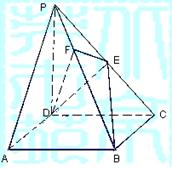
17．（12分）如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、

　　PC的中点．

　 （1）求证：EF∥平面PAD；

　 （2）求证：EF⊥CD；

　 （3）若ÐPDA＝45°，求EF与平面ABCD所成的角的大小．

18．（12分）在正方体中，如图Ｅ、Ｆ分别是

 ，ＣＤ的中点，

　 （1）求证：平面ADE；

　 （2）求．

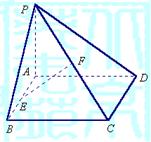
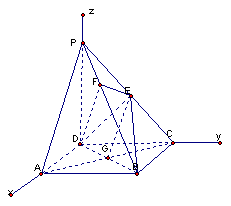
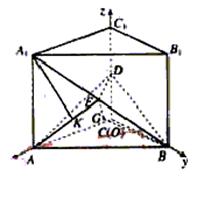
19．（14分）如图，在四棱锥中，底面ABCD是正方形，侧棱底面ABCD，

　　　，E是PC的中点，作交PB于点F.

　 （1）证明 平面；

　 （2）证明平面EFD；

　 （3）求二面角的大小．

20．（14分）如图，直三棱柱ABC—A₁B₁C₁中，底面是等腰直角三角形，∠ACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的垂心G.

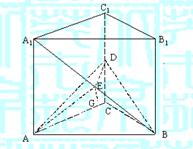
　 （1）求A₁B与平面ABD所成角的大小

（结果用反三角函数值表示）；

　 （2）求点A₁到平面AED的距离.

参考答案（六）

一、选择题（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	A	C	B	D	D	C	A	B	A	C

二、填空题（本大题共4小题，每小题6分，共24分）

11．　　　 12． 0　　  13． 　 14．0°

三、解答题（本大题共6题，共76分）

15．(12分) 证明： .　又，

即.……①　　　 .

　　　　 又，即.……②　

　　　　 由①+②得：即..

16．(12分) 解：(1) A(2, 2, 0)，B₁(2, 0, 2)，E(0, 1, 0)，D₁(0, 2, 2)

　　　　  (2)∵ ＝(0, -2, 2)，＝(0, 1, 2)　∴ ＝2，＝，·＝0－2＋4＝2,

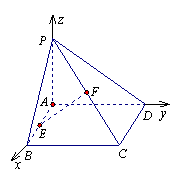∴ cos á，ñ ＝ ＝ ＝ ．∴ AB₁与ED₁所成的角的余弦值为．

17．(12分) 证：如图，建立空间直角坐标系A－xyz，设AB＝2a，

BC＝2b，PA＝2c，则：A(0, 0, 0)，B(2a, 0, 0)，C(2a, 2b, 0)，

　　　　 D(0, 2b, 0)，P(0, 0, 2c)　　∵ E为AB的中点，F为PC的中点　　　　　　　　　　　

　　　　 ∴ E (a, 0, 0)，F (a, b, c)

(1)∵ ＝(0, b, c)，＝(0, 0, 2c)，＝(0, 2b, 0)

　　　　 ∴ ＝(＋) ∴ 与、共面

　　　　 又∵ E Ï 平面PAD　　　　∴ EF∥平面PAD．

(2) 　 ∵ ＝(-2a, 0, 0 )　　　　∴ ·＝(-2a, 0, 0)·(0, b, c)＝0　　　　　　　　　

∴ CD⊥EF．

(3) 　 若ÐPDA＝45°，则有2b＝2c，即 b＝c，　　　　　　 ∴ ＝(0, b, b)，

　　　　 ＝(0, 0, 2b)　　　　　　　　 ∴ cos á，ñ＝＝　　　　　　　　　 ∴ á，ñ＝ 45°

　　　　 ∵ ⊥平面AC，∴ 是平面AC的法向量　 ∴ EF与平面AC所成的角为：90°－á，ñ＝ 45°．

18．(12分) 解：建立如图所示的直角坐标系，（1）不妨设正方体的棱长为1，

则D（0，0，0），A（1，0，0），（0，0，1），

　　　　 E（1，1，），F（0，，0），

　　　　 则＝（0，，－1），＝（1，0，0），　　

　　　　 ＝（0，1，），  则＝0，

　　　　 ＝0， ，.　　

　　　　 平面ADE.

（２）（1，1，1），C（0，1，0），故＝（1，0，1），＝（－1，－，－），

　　　　 ＝－1＋0－＝－，　　 ，，　　

则cos. .　　　　

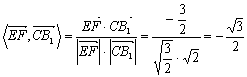19．（14分）解：如图所示建立空间直角坐标系，D为坐标原点.设

(1)证明：连结AC，AC交BD于G.连结EG.

　　　　 依题意得

　　　　 底面ABCD是正方形， 是此正方形的中心，

　　　　 故点G的坐标为且

　　　　 . 这表明.

　　　　 而平面EDB且平面EDB，平面EDB。

(2)证明：依题意得。又故　

　　　　 , 由已知，且所以平面EFD.

(3)解：设点F的坐标为则

　　　　 从而所以

　　　　 由条件知，即　　 解得 。

　　　　 点F的坐标为 且

　　　　 ,即，故是二面角的平面角.

　　　　 ∵且

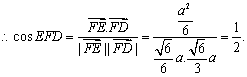
　　　　  ,所以，二面角C—PC—D的大小为

20．(14分) 解：（1）连结BG，则BG是BE在面ABD的射影，即∠A₁BG是A₁B与平面ABD所成的角. 如图所示建立坐标系，坐标原点为O，设CA=2a，

则A（2a，0，0），B（0，2a，0），D（0，0，1） A₁（2a，0，2）

E（a，a，1）　G（）.

，

，解得a=1.

.

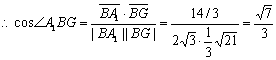A₁B与平面ABD所成角是.

（2）由（1）有A（2，0，0），A₁（2，0，2），E（1，1，1），D（0，0，1）

平面AA₁E，又ED平面AED.

∴平面AED⊥平面AA₁E，又面AED面AA₁E=AE，

∴点A在平面AED的射影K在AE上.

设，  则

由，即，　　　解得.

　　　　 ,即

即点A₁到平面AED的距离为.