2004－2005学年度下学期
高中学生学科素质训练
高二数学测试题（9）——排列组合及应用
YCY本试卷分第Ⅰ卷和第Ⅱ卷两部分，共150分.
第Ⅰ卷（选择题，共50分）
一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．若
为正整数，则乘积
（ ）
A．
B．
C．
D．
2．若直线
的系数
同时从0,1,2,3,5,7六个数字中取不同的值,则这些方程表示不同的直线条数
（ ）
A． 22 B． 30 C． 12 D． 15
3．四个编号为1，2，3，4的球放入三个不同的盒子里，每个盒子只能放一个球，编号为1的球必须放入，则不同的方法有 （ ）
A．12种 B．18种 C．24种 D．96种
4．用0，1，2，3，4组成没有重复数字的全部五位数中，若按从小到大的顺序排列，则数字12340应是第几个数 （ ）
A．6 B．9 C．10 D．8
5．把一个圆周24等分,过其中任意三个分点可以连成圆的内接三角形,其中直角三角形的个数是 （ ）
A．2024 B．264 C．132 D．122
6.由数字0，1，2，3，4，5可以组成无重复数字且奇偶数字相间的六位数的个数有（ ）
A．72 B．60 C．48 D．52
7. 3名男生与3名女生站在一排，如果要求男女生相间站，那么站法有 （ ）
A．36种 B．72种 C．108种 D．144种
8. 若
，则
的值为
（ ）
A．4 B．7 C．4或7 D．不存在
9．以正方体的顶点为顶点，能作出的三棱锥的个数是 （ ）
A．
B．
C．-6 D． 
10．从长度分别为1，2，3，4，5的五条线段中，任取三条的不同取法共有n种．在这些取法中，以取出的三条线段为边可组成的钝角三角形的个数为m，则
等于 （ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题，共100分）
二、填空题（本大题共4小题，每小题6分，共24分）
11．设含有8个元素的集合的全部子集数为S，其中由3个元素组成的子集数为T，
的值为___________．
12．有4个不同的小球，全部放入4个不同的盒子内，恰好有两个盒子不放球的不同放法的总数为 ．
13．甲、乙、丙、丁、戊5名学生进行某种劳动技术比赛，决出了第1到第5名的名次．甲、乙两名参赛者去询问成绩，回答者对甲说：“很遗憾，你和乙都未拿到冠军”，对乙说：“你当然不会是最差的”．从这个回答分析，5人的名次排列共可能有 （用数字作答）种不同情况．
14．一块并排10垄的田地中，选择2垄分别种植A．B两种作物，每种作物种植一垄．为有利于作物生长，要求A．B两种作物的间隔不小于6垄，则不同的选垄方法共有
种．
三、解答题（共计76分）
15．（12分）2002韩日世界杯足球赛参球队共32支，先组成8个小组进行单循环赛，决出16强（各组前2名），这16强队按确定程序进行淘汰赛决出前8名，再决出4强，直到决出冠军、亚军、第三、四名，共赛多少场？
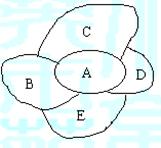
16．（12分）某市A有四个郊县B．C．D．E．（如图）,现有5种颜色，若要使每相邻的两块涂不同颜色，且每块只涂一种颜色，问有多少种不同的涂色方法？（14分）
|
17．（12分）用0，1，2，3，4，5组成没有重复数字的自然数，
（1）有多少个比201 345大？（2）有多少个是25的倍数的四位数？
18．（12分）排一张有5个歌唱节目和4个舞蹈节目的演出节目单,要求：
（1）任何两个舞蹈节目不相邻的排法有多少种？
（2）歌唱节目与舞蹈节目间隔排列的方法有多少种？
19．（14分）6本不同的书，按照以下要求处理，各有几种分法？
（1）一堆一本，一堆两本，一堆三本；
（2）甲得一本，乙得两本，丙得三本；
（3）一人得一本，一人得二本，一人得三本；
（4）平均分给甲、乙、丙三人；（5）平均分成三堆．
20．（14分）从1到9的九个数字中取三个偶数、四个奇数，试问：
（1）能组成多少个没有重复数字的七位数？
（2）上述七位数中三个偶数排在一起的有几个？
（3）（1）中的七位数中，偶数排在一起、奇数也排在一起的有几个？
（4）（1）中任意两偶然都不相邻的七位数有几个？
参考答案（九）
一．选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | A | B | C | B | B | B | C | D | B |
二．填空题（本大题共4小题，每小题6分，共24分）
11.
12．84
13． 54
14． 12
三、解答题（本大题共6题，共76分）
15．(12分)解：32支球队分成8组，每组4支球队，进行单循环赛，每组取前二名，一共应进行8×
=48,
16强队按程序进行淘汰赛决出前八名，应进行8场比赛，再决出4强，应进行4场比赛，决出冠军、亚军、三、四名，应进行4场比赛
故总计：48+8+4+4=64场比赛
16．(12分) 解：符合题意的涂色至少要3种颜色，分类如下
17．(12分)
（1）4P
-1=479 （2）
=21
18．(12分)
解：（1）先排歌唱节目有
种，歌唱节目之间以及两端共有6个位子，从中选4个放入舞蹈节目，共有
中方法，所以任两个舞蹈节目不相邻排法有：
＝43200.
（2） 先排舞蹈节目有
中方法，在舞蹈节目之间以及两端共有5个空位，恰好供5个歌唱节目放入．所以歌唱节目与舞蹈节目间隔排列的排法有：
＝2880种方法．
19．（14分）解：（1）先在6本书中任取一本．作为一本一堆，有
种取法，再从余下的五本书中任取两本，作为两本一堆，有
种取法，再后从余下三本取三本作为一堆，有
种取法，故共有分法=60种．
（2）由（1）知．分成三堆的方法有种，而每种分组方法仅对应一种分配方法，故甲得一本，乙得二本，丙得三本的分法亦为=60 种．
（3）由（1）知，分成三堆的方法有种，但每一种分组方法又有
不同的分配方案，故一人得一本，一人得两本，一人得三本的分法有=360（种）．
（4）3个人一个一个地来取书，甲从6本不同的书本中任取出2本的方法有
种，甲不论用哪一种方法取得2本书后，已再从余下的4本书中取书有
种方法，而甲、乙不论用哪一种方法各取2本书后，丙从余下的两本中取两本书，有
种方法，所以一共有
=90种方法．
（5）把6本不同的书分成三堆，每推二本与把六本不同的书分给甲、乙、丙三人，每人二本的区别在于，后者相当于把六本不同的书，平均分成三难后，再把每次分得的三堆书分给甲、乙、丙三个人．因此，设把六本不同的书，平均分成三堆的方法有
种，那么把六本不同的书分给甲、乙、丙三人每人2本的分法就应
种，由（4）知，把六本不同的书分给甲、乙、丙三人，每人2本的方法有 种．
所以
，则
（种）
20．(14分)解：（l）分步完成：第一步在4个偶数中取3个，可有
种情况；第二步在5个奇数中取4个，可有
种情况；第三步3个偶数，4个奇数进行排列，可有
种情况，所以符合题意的七位数有
个．
（2）上述七位数中，三个偶数排在一起的有个．
（3）上述七位数中，3个偶数排在一起，4个奇数也排在一起的有
个．
（4）上述七位数中，偶数都不相邻，可先把4个奇数排好，再将3个偶数分别插入5个空档，共有
个．