高二期中联合考试
数学 试卷
命题学校：五常高中 命题人：麻延明
一、选择题（
1、下列命题正确的是（ ）
A、直线a，b与直线
所成角相等，则a//b
B、直线a，b与平面α成相等角，则a//b
C、平面α，β与平面γ所成角均为直二面角，则α//β
D、直线a，b在平面α外，且a⊥α，a⊥b，则b//α
2、人们常见的地球仪的轴与水平桌面成66.5°角，那么地球仪表面距桌面最近的点总是在
A 南纬23.5°圈上 B 南纬66.5°圈上 C 南极上 D 赤道上
3、在
（
）展开式中，二项式系数最大的项
A．第n-1项 B．第n项
C．第n-1项与第n+1项 D．第n项与第n+1项
4、空间四点A、B、C、D共面但不共线，那么这四点中
A 必有三点共线 B 必有三点不共线
C 至少有三点不共线 D 不可能有三点共线
5、以正方体的顶点为顶点，能做出的三棱锥的个数是（ ）
A、
B、
C、-6 D、
6、在正方体A1B
A 
B 
C 
D 
7、已知a、b是两条直线，
、
是两个平面，有下列4个命题；
①若a∥b,b
则a∥; ②若a ⊥b,a⊥,b
则b∥ ③若⊥，
a⊥,b⊥则a⊥b ④若a 、b异面，a,b,a∥则∥其中真命题有：
A ①② B ②③ C ③④ D ②④
8、以等腰直角三角形ABC的斜边BC边上的高AD为折痕，将
ABD折起，使折起后的ABC恰成等边三角形，则二面角C-AD-B的平面角等于：
A 
B 
C 
D 
9、氨基酸的排列顺序是决定蛋白质多样性的原因之一，某肽链由7种不同的氨基酸构成，若只改变其中3种氨基酸的位置，其他4种不变，则不同的改变方法共有（ ）
A、210种 B、126种 C、70种 D、35种
10、从1、2、3、4、5这五个数字中任取3个组成无重复数字的三位数，当三个数字有2和3时，则2需排在3的前面(不一定相邻)，这样的三位数有（ ）
A、9个 B、15个 C、45个 D、51个
11、棱长都等于2的直平行六面体
中，∠BAD＝60°，则对角线
与侧面
所成角的正弦值为（ ）
A、
B、
C、
D、
12、甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为
，再由乙猜甲刚才所想的数字，把乙猜的数字记为
，
，若
，就称甲乙“心有灵犀”。现任意找两人玩这个游戏，得出他们“心有灵犀”的概率为（ ）
A、7/25
B 、9/
二、填空题（
13、若
a0+a1x+a2x2…+a2006x2006(x
R)则（a0+a1）+(a0+a2)+…+(a0+a2006)
= (用数字作答)
14、空间12个点，其中5个点共面，此外无任何4个点共面，这12个可决定_________________个不同的平面。
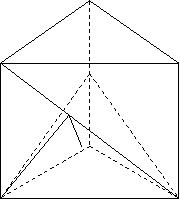
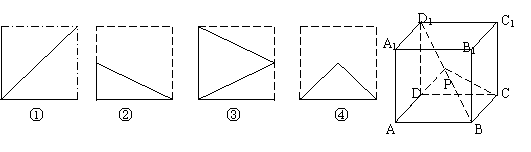15、如图,在正方体ABCD-A1B
16、在平面几何里，有勾股定理：“设ABC的两边AB、AC互相垂直，则AB2+AC2=BC
拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得出正确的结论是：“设三棱锥A—BCD的三个侧面ABC，ACD，ADB两面相互垂直，则______________________________________.
三、解答题（
17、（本小题满分12分）
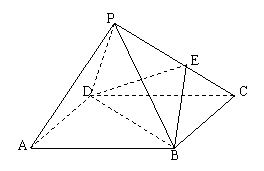如图,已知四棱锥
的侧面是正三角形, 
是
的中点求证:
(1)PA 
平面BDE；
(2) 平面BDE
平面PAC。
18、如图，在正方体ABCD—A1B
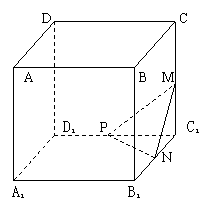⑴求证: AP⊥MN；
⑵求证:平面MNP∥平面A1BD。
19、（本小题满分12分）
袋子内装有大小相同的15个小球，其中有
个红球，5个黄球，其余为白球。
(1)从中任意摸出2个小球，求得到2个都是黄球的概率；
(2)如果从中任意摸出2个小球，得到都是红球或都是黄球的概率为
，求红球的个数；
(3)根据(2)的结论，试计算从袋中任意摸出3个小球得到至少有1个白球的概率。
20、文科做（本小题满分12分）
求（2x-1）5的展开式中（1）各项系数之和；（2）各项的二项式系数之和；（3）偶数项的二项式系数之和；
20、理科做（本小题满分12分）
已知
展开式中，x的系数为11求：
(1)
的展开式中, 
的系数的最小值；
(2)当的系数取最小值时，求展开式中
的奇数次幂项的系数和。
21、（本小题满分12分）
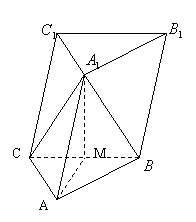
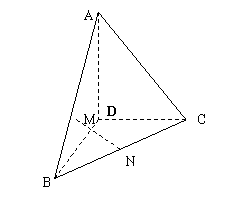如图，四面体ABCD的棱AD、BD、CD 两两垂直，AD＝9, BD=6,CD=8,M为△ABD的重心，N为BC的中点。
(1)求MN与平面BCD所成的角；
(2)求三棱锥M-ABC的体积；
(3)求平面BCD和平面ABC所成的角。
22、文科做（本小题满分14分）
已知斜三棱柱ABC—A1B
M为BC的中点，且点M到侧面AA1B1B的距离为
，
（1）求证：平面A1AM⊥平面A1BC；
（2）求二面角A1—AB—C的大小；
（3）求点B到平面ACC
22、理科做（本小题满分14分）
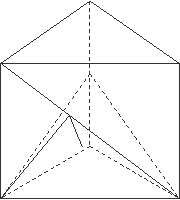
如图，在直三棱柱ABC—A1B
AA1=2， D、E分别是CC1与A1B的中点，点E在平面ABD上的射影是ABD的重心G。
⑴求A1B与平面ABD所成角的大小（文科求正弦，理科反三角函数表示）
⑵求点A1到平面AED的距离
C1
A1 B1
D
E
C
G
A
B
高二期中联合考试
|
命题学校： 五常高中 命题人： 麻延明
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||
一、选择题（
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（
13、 14、
15、 16、
三、解答题（
17、（本小题满分12分）
18、（本小题满分12分）
19、（本小题满分12分）
20、（本小题满分12分）
21、（本小题满分12分）
22、（本小题满分14分）
高二期中联合考试--数学答案
一、选择题（
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | D | B | D | B | B | D | C | D | D | A |
二、填空题（
13、 2006 14、211 15、①④ 16、
+
+
=
三、解答题（
17、（本小题满分12分）
证明：（1）连结AC交BD于0点，连结EO
则O为AC的中点，则有OE为中位线∴OE‖AP
∴
‖
-------------------------------------------------------------------------6分
（2）在△BCP中，有BE⊥PC
在△DCP中，有DE⊥PC又DE∩BE=E故有PC⊥面BDE
又PC在平面PAC上
∴平面BDE 平面PAC----------------------------------------------------------------------12分
18、（本小题满分12分）
（1）连结BC1、B
又B
⑵ 连结B1D1，
∵P、N分别是D
∴ PN∥BD 又PN不在平面A1BD内， ∴PN∥平面A1BD同理MN∥平面A1BD
又PN∩MN=N ∴ 平面PMN∥平面A1BD
19、解：（I）从15个小球中摸出2个小球都是黄球的概率为 
---------------4分
（II）设有n个红球，由题意知
---------------6分
-----------------------8分
（III）由（II）知有4个红球，故有6个白球，设摸出3个小球得到至少有1个白球为事件A
则无白球的概率为
------------------------------10分
-----------------------------12
20、理科（本小题满分12分）
解：（1）∵展开式中，x的系数为11.
∴
即 
（2分）
故
的系数为
（
）当
或
时，此式也成立．
（4分）
又∵
∴当
或6时，
（6分）
（2）当或6时，
（8分）
设奇数次幂项的系数和为u，偶数次幂项的系数和为v，则
（10分）
∴
（12分）
20、文科注：
21、（本小题满分12分）
解（1）以DB、DC、DA为ｘ轴、y轴、z轴建立空间直角坐标系Ｄ－xyz。则A（0，0，9）B（6，0，0）C（0，8，0）D（0、0、0）―――――――――――――――１分
M为三角形ABD的重心，所以M（２，０，３）N是BC的中点，所以N（３，４，０）所以
设面ＢＣＤ的法向量为
――――――――――――――４分
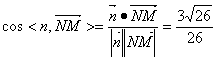――――――――――――――――――――－５分
设MN与平面BCD所成的角为，则
。所以MN与平面所成的角为
―――――――――――――――――――――――――――――――――――――６分
（２）
连接ＤＭ延长AB于E点，则
则点Ｍ到平面ABC的距离
是点Ｄ到面ABC距离h的
，即＝
，所以
――――１２分
22、文科（本小题满分14分）
解（1）证
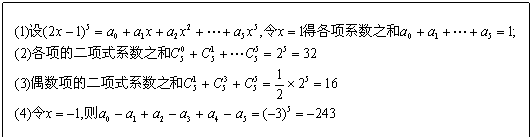―――――――――――――――――――――――――――――――――――――――３分
|
| |
∴ G∈DF，在Rt△EFD,EF2=FG·FD=FD2, ∵ EF=1 ∴ DF=
于是ED=
， EG=
∵ FC=ED= ∴ AB=2，A1B=2
EB= ∴ sin∠EBG=
∴ A1B与平面ABD所成的角是arcsin
⑵连结A1D，有∨A1-ADE=∨D-AA1E ∵ED⊥AB， ED⊥EF，又EF∩AB=F
∴ ED⊥平面A1AB，设A1到平面AEB的距离为h,则S△AED·h=S△A1AE.ED
又
S
=
=
A。AB=， S△AED=
∴ h=
即A1到平面AED的距离为
C1
A1 B1
D
F
G C